Material to support teaching in Environmental Science at The University of Western Australia

Units ENVT3361, ENVT4461, and ENVT5503

Relationships pages: Correlations | Simple linear regression | Grouped linear regression | Multiple linear regression

Introduction

Another way we can improve the ability of a linear regression model, as compared with a simple regression model, is to allow prediction of our dependent variable with more than one independent variable – the idea of multiple predictors, or multiple regression. (We have already examined the use of grouped linear regression to improve prediction relative to simple linear regression.)

Developing a multiple linear regression model

NOTE: This section on multiple regression is optional – it is more advanced material which we will not cover in class, but which may be useful for analysing data from the class project.

Sometimes the unexplained variation in our dependent variable (i.e. the residuals) may be able to be explained in part by one or more additional predictors in our data. If we suspect this to be true, we can add predictors in a multiple linear regression model.

Multiple regression models predict the value of one variable (the dependent variable) from two or more predictor variables (or just 'predictors'). They can be very useful in environmental science, but there are several steps we need to take to make sure
that we have a valid model.

In this example we're going to develop a regression model to predict gadolinium (Gd) concentrations in sediment from several predictors. It makes sense to choose predictors that represent bulk sediment properties that could plausibly control trace element concentrations. So, we choose variables like pH, EC, organic carbon, cation exchange capacity, and some major elements as predictors (but NOT other trace elements; different trace elements may be highly correlated (due to common sources & sinks), but their concentrations are most likely too low to control the concentration of anything else!)

Since we don't have organic carbon or cation exchange capacity in this dataset, and there are many missing values for EC, our initial predictors will be Al, Ca, Fe, K, Mg, Na, pH, and S. Both the predictors and dependent variable need to be appropriately transformed before we start! (Remember that linear regression assumptions are based on the residuals, but we are less likely to fulfil these assumptions if our variables are very skewed. A good option is often to log₁₀-transform variables if necessary.)

Also, some of our initial predictors may be highly correlated (co-linear) with each other. In multiple regression, we don't want to include co-linear predictors, since then we'll have two (or more) predictors which effectively contain the same information – see below.

For practical purposes, we prefer [linear] regression models which are:

good at prediction (i.e. having the greatest possible R² value);
as simple as possible (i.e. not having predictors which a co-linear, and only accepting a more complex model if it significantly improves prediction, e.g., by anova());
meet the assumptions of linear regression (although we have argued previously that even if some assumptions are not met, a regression model can still be used for prediction).

Read input data

As previously, our first step is to read the data, and change anything we need to:

git <- "https://github.com/Ratey-AtUWA/Learn-R-web/raw/main/"
afs1923 <- read.csv(paste0(git,"afs1923.csv"), stringsAsFactors = TRUE)
# re-order the factor levels
afs1923$Type <- factor(afs1923$Type, levels=c("Drain_Sed","Lake_Sed","Saltmarsh","Other"))
afs1923$Type2 <- 
  factor(afs1923$Type2, 
         levels=c("Drain_Sed","Lake_Sed","Saltmarsh W","Saltmarsh E","Other"))

Assess collinearity between initial set of predictors

First we inspect the correlation matrix. It's useful to include the dependent variable as well, just to see which predictors are most closely correlated.

(We try to generate a 'tidier' table by restricting numbers to 3 significant digits, and making the values = 1 on the diagonal NA. We don't need to use corTest() from the psych package, since we're not so interested in P-values for this purpose.)

Note that all variables are appropriately transformed!
You will need to do this yourself...

cor0 <- 
  cor(afs1923[,c("Al","Ca.log","Fe","K","Mg.pow","Na.pow","pH","S.log","Gd.pow")],
   use="pairwise.complete")
cor0[which(cor0==1)] <- NA         # change diagonal to NA
print(round(cor0,3), na.print="")  # round to 3 decimal places and print nothing for NAs

##            Al Ca.log    Fe      K Mg.pow Na.pow     pH  S.log Gd.pow
## Al             0.075 0.217  0.747  0.498  0.350 -0.126 -0.005  0.787
## Ca.log  0.075        0.235  0.173  0.447  0.315  0.288  0.382 -0.013
## Fe      0.217  0.235        0.321  0.486  0.458  0.062  0.368  0.286
## K       0.747  0.173 0.321         0.794  0.738 -0.122  0.281  0.657
## Mg.pow  0.498  0.447 0.486  0.794         0.939  0.020  0.527  0.427
## Na.pow  0.350  0.315 0.458  0.738  0.939        -0.095  0.566  0.339
## pH     -0.126  0.288 0.062 -0.122  0.020 -0.095         0.068 -0.221
## S.log  -0.005  0.382 0.368  0.281  0.527  0.566  0.068        -0.014
## Gd.pow  0.787 -0.013 0.286  0.657  0.427  0.339 -0.221 -0.014

rm(cor0)                           # tidy up

The rule of thumb we use is that:

If predictor variables are correlated with Pearson's r ≥ 0.8 or r ≤ -0.8, then the collinearity is too large and one of the correlated predictors should be omitted

In the correlation table above this doesn't apply to the correlation between [transformed] Na and Mg, with r=0.94. In this example we will run two versions of the model, one keeping both Na and Mg, and one omitting Mg.

We have just added a fifth assumption for linear regression models specifically for multiple regression:

Independent variables (predictors) should not show significant covariance

In either case, whether we run the model with or without omitting predictors, it's a good idea to calculate Variance Inflation Factors on the predictor variables in the model (see below) which can tell us if collinearity is a problem.

Generate multiple regression model for Gd (co-linear predictors NOT omitted)

We first delete any observations (rows) with missing (NA) values, otherwise when we change the number of predictors later, we may not have the same number of observations for all models, in which case we can't compare them.

# make new data object containing relevant variables with no missing values
afs1923_multreg <- na.omit(afs1923[c("Gd.pow","Al","Ca.log","Fe","K","Mg.pow",
                                     "Na.pow","pH","S.log")])
row.names(afs1923_multreg) <- NULL  # reset row indices
# run model using correctly transformed variables
lm_multi <- lm(Gd.pow ~ pH + Al + Ca.log + Fe + K + Mg.pow + 
               Na.pow + S.log, data=afs1923_multreg)
summary(lm_multi)

## 
## Call:
## lm(formula = Gd.pow ~ pH + Al + Ca.log + Fe + K + Mg.pow + Na.pow + 
##     S.log, data = afs1923_multreg)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.29003 -0.27205 -0.03327  0.25159  1.35793 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  9.574e-01  3.441e-01   2.783  0.00576 ** 
## pH          -1.904e-02  3.248e-02  -0.586  0.55809    
## Al           4.044e-05  3.494e-06  11.574  < 2e-16 ***
## Ca.log       6.936e-02  9.514e-02   0.729  0.46662    
## Fe           7.415e-06  1.405e-06   5.277 2.63e-07 ***
## K            1.031e-04  4.078e-05   2.529  0.01200 *  
## Mg.pow      -1.529e-02  5.364e-03  -2.850  0.00469 ** 
## Na.pow       3.311e-02  1.195e-02   2.772  0.00595 ** 
## S.log       -7.455e-02  6.588e-02  -1.132  0.25875    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3996 on 281 degrees of freedom
## Multiple R-squared:  0.6976, Adjusted R-squared:  0.6889 
## F-statistic: 81.01 on 8 and 281 DF,  p-value: < 2.2e-16

Note that the null hypothesis probability Pr(>|t|) for some predictors (pH, Ca.log and S.log) is ≥ 0.05, so we can't reject the null hypothesis – that this predictor has no effect on the dependent variable.

Calculate variance inflation factors (VIF) for the predictors in the 'maximal' model

To calculate variance inflation factors we use the function vif() from the car package. The input for vif() is a lm object (in this case lm_multi).

require(car)
{cat("Variance Inflation Factors\n")
vif(lm_multi)}

## Variance Inflation Factors
##        pH        Al    Ca.log        Fe         K    Mg.pow    Na.pow     S.log 
##  1.352595  3.484229  1.709828  1.250150  5.115344 17.110451 13.467308  1.613731

The VIF could be considered the "penalty" from having 2 or more predictors which (since they contain the same information) don't decrease the unexplained variance of the model, but add unnecessary complexity. A general rule of thumb is that if VIF > 4 we need to do some further investigation, while serious multi-collinearity exists requiring correction if VIF > 10 (Hebbali, 2018). As we probably expected from the correlation coefficient (above), VIFs for both Na and Mg are >10 in this model, which is too high, so we need to try a model which omits Na or Mg (we'll choose Mg), since vif ≥ 10 suggests we remove one . . .

Generate multiple regression model for Gd, omitting co-linear predictors

# make new data object containing relevant variables with no missing values
# run model using correctly transformed variables (omitting co-linear predictors)
lm_multi2 <- lm(Gd.pow ~ pH + Al + Ca.log + Fe + K + 
               Na.pow + S.log, data=afs1923_multreg)
summary(lm_multi2)

## 
## Call:
## lm(formula = Gd.pow ~ pH + Al + Ca.log + Fe + K + Na.pow + S.log, 
##     data = afs1923_multreg)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.19739 -0.25259 -0.01869  0.23688  1.42385 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.411e+00  3.089e-01   4.569 7.34e-06 ***
## pH          -4.798e-02  3.124e-02  -1.536   0.1257    
## Al           3.603e-05  3.171e-06  11.359  < 2e-16 ***
## Ca.log      -5.353e-02  8.588e-02  -0.623   0.5336    
## Fe           6.754e-06  1.403e-06   4.813 2.43e-06 ***
## K            8.635e-05  4.086e-05   2.113   0.0354 *  
## Na.pow       3.623e-03  6.050e-03   0.599   0.5497    
## S.log       -6.518e-02  6.662e-02  -0.978   0.3288    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4046 on 282 degrees of freedom
## Multiple R-squared:  0.6888, Adjusted R-squared:  0.6811 
## F-statistic: 89.17 on 7 and 282 DF,  p-value: < 2.2e-16

Note that again the null hypothesis probability Pr(>|t|) for some predictors (pH, Ca.log and S.log) is ≥ 0.05, so we can't reject the null hypothesis – that these predictors have no effect on the dependent variable.

Calculate variance inflation factors (VIF) for the model omitting co-linear predictors

require(car)
{cat("Variance Inflation Factors\n")
vif(lm_multi2)}

## Variance Inflation Factors
##       pH       Al   Ca.log       Fe        K   Na.pow    S.log 
## 1.220446 2.799425 1.358736 1.216093 5.008973 3.368022 1.609711

With the co-linear variable(s) omitted (on the basis of |Pearson's r| > 0.8 and vif > 10), we now have no VIFs > 10. We do have one vif > 4 for K, but we'll retain this predictor as it may represent illite-type clay minerals which can be reactive to trace elements like Gd in sediment. We now move on to stepwise refinement of our [new] 'maximal' model...

Stepwise refinement of maximal multiple regression model (omitting co-linear predictors)

We don't want to have too many predictors in our model – just the predictors which explain significant proportions of the variance in our dependent variable. The simplest possible model is best! In addition, our data may be insufficient to generate a very complex model; one rule-of-thumb suggests 10-20 observations are needed to calculate coefficients for each predictor. Reimann et al. (2008) recommend that the number of observations should be at least 5 times the number of predictors. So, we use a systematic stepwise procedure to test variations of the model, which omits unnecessary predictors.

lm_stepwise <- step(lm_multi2, direction="both", trace=0)
summary(lm_stepwise)

## 
## Call:
## lm(formula = Gd.pow ~ pH + Al + Fe + K, data = afs1923_multreg)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.19924 -0.25712 -0.02805  0.23895  1.43567 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.133e+00  2.016e-01   5.619 4.57e-08 ***
## pH          -5.898e-02  2.888e-02  -2.043 0.042007 *  
## Al           3.626e-05  2.787e-06  13.010  < 2e-16 ***
## Fe           6.491e-06  1.318e-06   4.926 1.42e-06 ***
## K            9.172e-05  2.742e-05   3.345 0.000932 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4038 on 285 degrees of freedom
## Multiple R-squared:  0.6868, Adjusted R-squared:  0.6824 
## F-statistic: 156.2 on 4 and 285 DF,  p-value: < 2.2e-16

require(car)
{cat("==== Variance Inflation Factors ====\n")
vif(lm_stepwise)}

## ==== Variance Inflation Factors ====

##       pH       Al       Fe        K 
## 1.047243 2.171232 1.076866 2.264963

In the optimised model, we find that the stepwise procedure has generated a new model with fewer predictor variables. You should notice that the p-values (Pr(>|t|)) for intercept and predictors are all now ≤ 0.05, so we can reject the null hypothesis for all predictors (i.e. none of them have 'no effect' on Gd). Our VIFs are now all close to 1, meaning negligible collinearity between predictors.

From the correlation matrix we made near the beginning, we see that Gd was most strongly correlated with Al (r = 0.787). In the interests of parsimony, it would be sensible to check whether our multiple regression model is actually better than a simple model just predicting Gd from Al:

lmGdAl <- lm(Gd.pow ~ Al, data = afs1923_multreg)
summary(lmGdAl)

## 
## Call:
## lm(formula = Gd.pow ~ Al, data = afs1923_multreg)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.25175 -0.29628 -0.07589  0.28599  1.54474 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1.005e+00  6.920e-02   14.52   <2e-16 ***
## Al          4.539e-05  2.037e-06   22.28   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4349 on 288 degrees of freedom
## Multiple R-squared:  0.6329, Adjusted R-squared:  0.6317 
## F-statistic: 496.6 on 1 and 288 DF,  p-value: < 2.2e-16

Our simple model has R² ≃ 63%, which is quite close to the ≃ 68% from the multiple linear regression, so we should check if multiple regression really does give an improvement. Since the simple and multiple models are nested we can use both AIC() and anova():

AIC(lmGdAl, lm_stepwise)
cat("\n-------------------------------------\n")
anova(lmGdAl, lm_stepwise)

##             df      AIC
## lmGdAl       3 344.0136
## lm_stepwise  6 303.9756
## 
## -------------------------------------
## Analysis of Variance Table
## 
## Model 1: Gd.pow ~ Al
## Model 2: Gd.pow ~ pH + Al + Fe + K
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    288 54.466                                  
## 2    285 46.470  3    7.9951 16.344 7.902e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

In this example, the lower AIC and anova p-value ≤ 0.05 support the idea that the multiple regression model (lm_stepwise) describes our data better.

It's always a good idea to run diagnostic plots (see Figure 1 below) on a regression model (simple or multiple), to check for (i) any systematic trends in residuals, (ii) normally distributed residuals (or not), and (iii) any unusually influential observations.

Regression diagnostic plots

par(mfrow=c(2,2), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.6,0.5,0), font.lab=2, font.main=3, 
    cex.main=0.8, tcl=-0.2)
plot(lm_stepwise, col=4)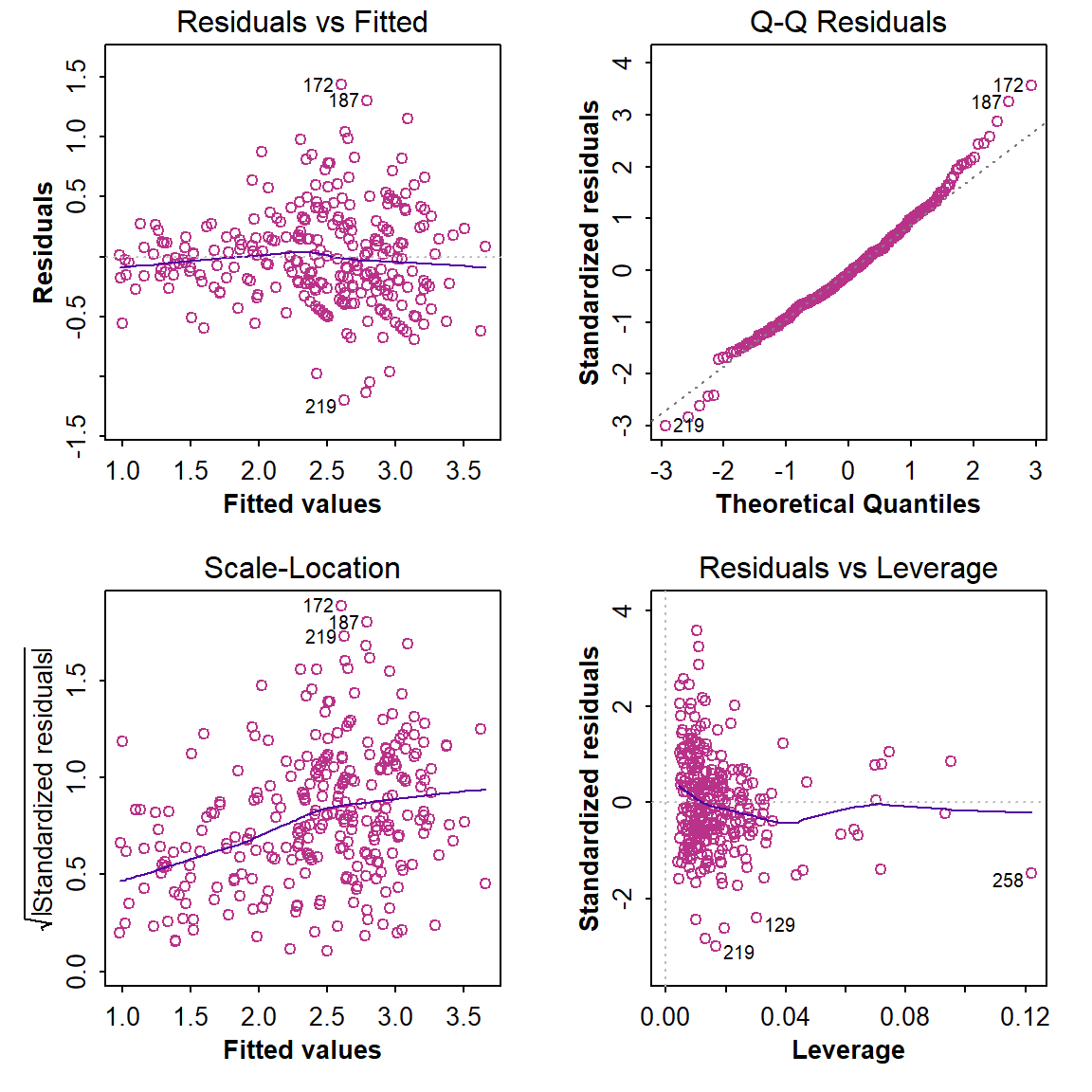

Figure 1: Diagnostic plots for the optimal multiple regression model following backward-forward stepwise refinement.

par(mfrow=c(1,1))

The optimal model is Gd.pow ~ Al.pow + Ca.pow + Fe.pow + S.pow, where suffixes .pow and .log represent power- and log₁₀-transformed variables respectively. The point labelled 78 does look problematic...

require(lmtest)
require(car)
cat("------- Residual autocorrelation (independence assumption):")
bgtest(lm_stepwise) # Breusch-Godfrey test for autocorrelation (independence)
cat("\n------- Test of homoscedasticity assumption:")
bptest(lm_stepwise) # Breusch-Pagan test for homoscedasticity
cat("\n------- Test of linearity assumption:")
raintest(lm_stepwise) # Rainbow test for linearity
cat("\n------- Bonferroni Outlier test for influential observations:\n\n")
outlierTest(lm_stepwise) # Bonferroni outlier test for influential observations
cat("\n------- Test distribution of residuals:\n")
shapiro.test(lm_stepwise$residuals) # Shapiro-Wilk test for normality
cat("\n------- Cook's Distance for any observations which are possibly too influential:\n")
summary(cooks.distance(lm_stepwise)) # Cook's Distance
cat("\n------- Influence Measures for any observations which are possibly too influential:\n")
summary(influence.measures(lm_stepwise))

## ------- Residual autocorrelation (independence assumption):
##  Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  lm_stepwise
## LM test = 62.536, df = 1, p-value = 2.616e-15
## 
## 
## ------- Test of homoscedasticity assumption:
##  studentized Breusch-Pagan test
## 
## data:  lm_stepwise
## BP = 15.786, df = 4, p-value = 0.003321
## 
## 
## ------- Test of linearity assumption:
##  Rainbow test
## 
## data:  lm_stepwise
## Rain = 1.0326, df1 = 145, df2 = 140, p-value = 0.4245
## 
## 
## ------- Bonferroni Outlier test for influential observations:
## 
## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
##     rstudent unadjusted p-value Bonferroni p
## 172 3.650077         0.00031196     0.090468
## 
## ------- Test distribution of residuals:
## 
##  Shapiro-Wilk normality test
## 
## data:  lm_stepwise$residuals
## W = 0.98593, p-value = 0.006173
## 
## 
## ------- Cook's Distance for any observations which are possibly too influential:
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 2.800e-07 2.798e-04 1.115e-03 3.166e-03 2.955e-03 6.105e-02 
## 
## ------- Influence Measures for any observations which are possibly too influential:
## Potentially influential observations of
##   lm(formula = Gd.pow ~ pH + Al + Fe + K, data = afs1923_multreg) :
## 
##     dfb.1_ dfb.pH dfb.Al dfb.Fe dfb.K dffit   cov.r   cook.d hat    
## 5   -0.05   0.06   0.01  -0.04   0.00 -0.07    1.05_*  0.00   0.04  
## 15  -0.17   0.14   0.05   0.05   0.02 -0.18    1.08_*  0.01   0.06_*
## 49   0.00   0.00   0.01   0.03  -0.02  0.04    1.05_*  0.00   0.04  
## 95  -0.07   0.06   0.16  -0.10   0.02  0.30    0.89_*  0.02   0.01  
## 129  0.17  -0.15  -0.38   0.01   0.29 -0.43_*  0.95_*  0.04   0.03  
## 146 -0.05   0.01  -0.06   0.28  -0.01  0.30    1.08_*  0.02   0.07_*
## 147 -0.05   0.03  -0.06   0.20   0.01  0.22    1.08_*  0.01   0.07_*
## 148 -0.02   0.01  -0.03   0.08   0.01  0.09    1.06_*  0.00   0.05  
## 150 -0.08   0.05  -0.05   0.25  -0.02  0.28    1.11_*  0.02   0.10_*
## 154  0.03  -0.05  -0.07   0.19   0.01  0.21    1.08_*  0.01   0.07_*
## 161  0.10  -0.10  -0.01  -0.05   0.04  0.20    0.91_*  0.01   0.01  
## 172  0.12  -0.10  -0.19  -0.09   0.27  0.37    0.82_*  0.03   0.01  
## 173  0.05  -0.08   0.05   0.13  -0.08  0.22    0.92_*  0.01   0.01  
## 176  0.07  -0.04   0.01  -0.06  -0.03  0.17    0.92_*  0.01   0.00  
## 187  0.22  -0.23  -0.06  -0.05   0.13  0.35    0.85_*  0.02   0.01  
## 197  0.08  -0.02  -0.18  -0.11   0.16  0.24    0.95_*  0.01   0.01  
## 212  0.03   0.03  -0.24  -0.27   0.32 -0.39    1.06_*  0.03   0.07_*
## 215  0.01  -0.01  -0.01   0.00   0.00  0.01    1.09_*  0.00   0.07_*
## 217 -0.19   0.20   0.12  -0.01  -0.17 -0.33    0.89_*  0.02   0.01  
## 219  0.10  -0.07   0.16  -0.26  -0.16 -0.40    0.88_*  0.03   0.02  
## 220  0.07  -0.09   0.15   0.14  -0.31 -0.37    0.92_*  0.03   0.02  
## 221  0.06  -0.08   0.14  -0.01  -0.17 -0.25    0.92_*  0.01   0.01  
## 233  0.06  -0.07   0.07   0.04  -0.12 -0.14    1.08_*  0.00   0.06_*
## 257  0.01  -0.01   0.05  -0.04  -0.03 -0.07    1.12_*  0.00   0.09_*
## 258  0.13  -0.14   0.42  -0.21  -0.39 -0.55_*  1.12_*  0.06   0.12_*
## 259  0.05  -0.07   0.13  -0.01  -0.12 -0.17    1.07_*  0.01   0.06_*

Multiple regression effect plots

require(effects)
plot(allEffects(lm_stepwise, confidence.level=0.95))

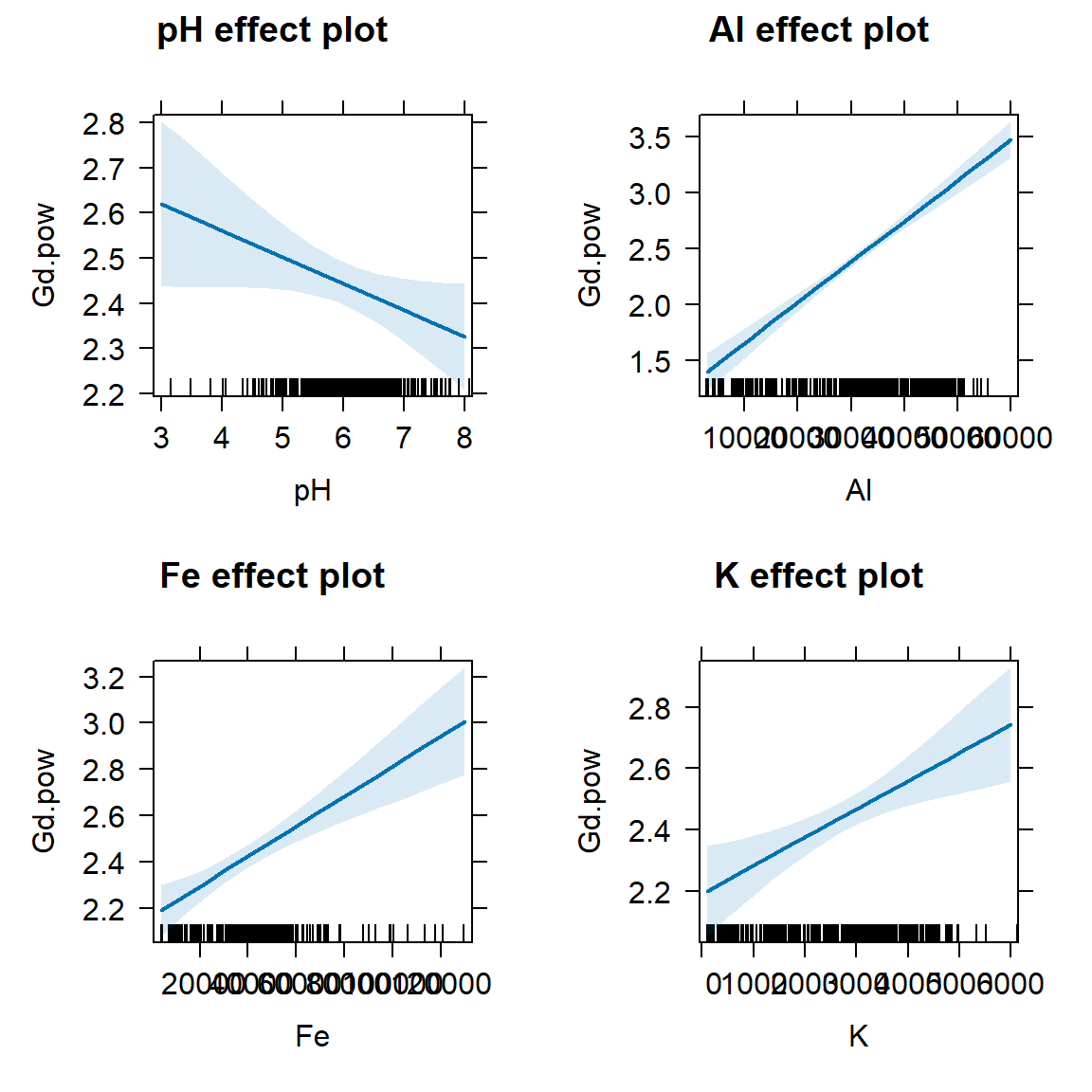
Figure 2: Effect plots for individual predictors in the optimal multiple regression model following backward-forward stepwise refinement. Light blue shaded areas on plots represent 95% confidence limits.

Scatterplot of observed vs. fitted values

An 'observed vs. fitted' plot (Figure 3) is a way around trying to plot a function with multiple predictors (i.e. multiple dimensions)! We can get the fitted values since these are stored in the lm object, in our case lm_stepwise in an item called lm_stepwise$fitted.values. We also make use of other information stored in the lm object, by calling summary(lm_stepwise)$adj.r.squared. Finally we use the predict() function with synthetic data in a dataframe newPreds to generate confidence and prediction intervals for out plot.

newPreds <- data.frame(Al=seq(0, max(afs1923_multreg$Al), l=100),
             Fe=seq(0, max(afs1923_multreg$Fe), l=100),
             K=seq(0, max(afs1923_multreg$K), l=100),
             pH=seq(min(afs1923_multreg$pH)*0.9, max(afs1923_multreg$pH), l=100))
conf1 <- predict(lm_stepwise, newPreds, interval = "conf")
conf1 <- conf1[order(conf1[,1]),]
pred1 <- predict(lm_stepwise, newPreds, interval="prediction")
pred1 <- pred1[order(pred1[,1]),]
par(mar=c(4,4,1,1), mgp=c(2,0.5,0), font.lab=2, cex.lab=1, 
    lend="square", ljoin="mitre")
plot(afs1923_multreg$Gd.pow ~ lm_stepwise$fitted.values,
     xlab="Gd.pow predicted from regression model",
     ylab="Gd.pow measured values", type="n")
mtext(side=3, line=-5.5, adj=0.05, col="blue3",
      text=paste("Adjusted Rsq =",signif(summary(lm_stepwise)$adj.r.squared,3)))
# lines(conf1[,1], conf1[,2], lty=2, col="red")
# lines(conf1[,1], conf1[,3], lty=2, col="red")
polygon(c(pred1[,1],rev(pred1[,1])), c(pred1[,2],rev(pred1[,3])), 
        col="#2000e040", border = "transparent")
polygon(c(conf1[,1],rev(conf1[,1])), c(conf1[,2],rev(conf1[,3])), 
        col="#ff000040", border = "transparent")
abline(0,1, col="gold4", lty=2, lwd=2)
points(afs1923_multreg$Gd.pow ~ lm_stepwise$fitted.values,
       pch=3, lwd=2, cex=0.8, col="blue3")
legend("topleft", legend=c("Observations","1:1 line"), col=c("blue3","gold4"), 
       text.col=c("blue3","gold4"), pch=c(3,NA), lty=c(NA,2), pt.lwd=2, lwd=2, 
       box.col="grey", box.lwd=2, inset=0.02, seg.len=2.7, y.intersp=1.2)
legend("bottomright", bty="n", title="Intervals", pch=15, pt.cex=2, 
       legend=c("95% confidence", "95% prediction"), col=c("#ff000040", "#2000e040"))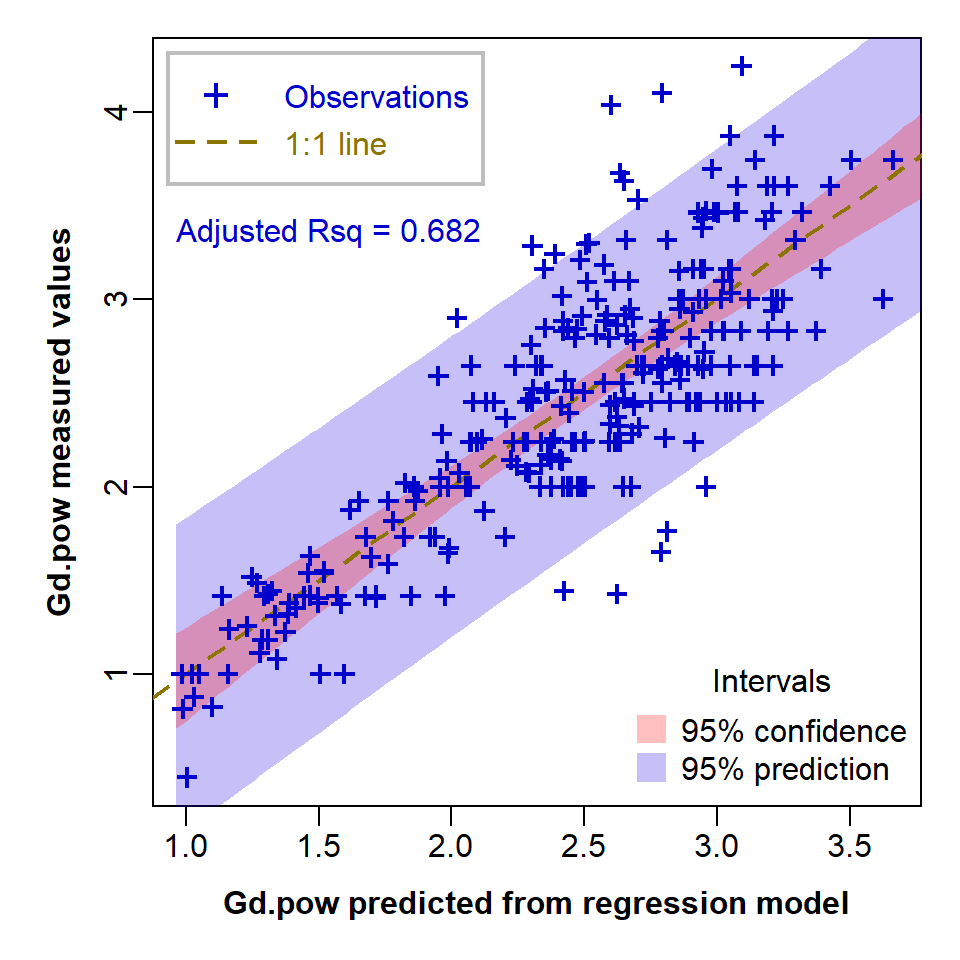

Figure 3: Measured (observed) vs. predicted values in the optimal multiple regression model, showing uncertainty intervals.

Some brief interpretation

The adjusted R-squared value of the final model is 0.682, meaning that 68.2%, about two-thirds, of the variance in Gd is explained by variance in the model's predictors. (The remaining 31.8% of variance must therefore be due to random variations, or 'unknown' variables not included in our model.)
From the model coefficients and the effect plots we can see that Gd increases as Al, Fe, and K increase, but Gd decreases as pH increases. This agrees with the relationships determined by correlation (see above); Gd is positively correlated with Ca, Fe, and S, and negatively correlated with pH.
(Note that this is not always the case - sometimes a predictor can be significant in a multiple regression model, but not individually correlated with the dependent variable!)
Although we can't attribute a causal relationship to correlation or regression relationships, the observed effects in our model are consistent with real phenomena. For example, gadolinium and other rare earth elements are positively related to iron (Fe) in other estuarine sediments; see Morgan et al. (2012). We also know that rare-earth elements in estuarine sediments are often associated with clays (Marmolejo-Rodríguez et al., 2007; clays are measured by Al in our data, since clays are aluminosilicate minerals).

References

Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences, Second Edition. Erlbaum Associates, Hillsdale, NJ, USA.

Marmolejo-Rodríguez, A. J., Prego, R., Meyer-Willerer, A., Shumilin, E., & Sapozhnikov, D. (2007). Rare earth elements in iron oxy-hydroxide rich sediments from the Marabasco River-Estuary System (pacific coast of Mexico). REE affinity with iron and aluminium. Journal of Geochemical Exploration, 94(1-3), 43-51. https://doi.org/10.1016/j.gexplo.2007.05.003

Morgan, B., Rate, A. W., Burton, E. D., & Smirk, M. (2012). Enrichment and fractionation of rare earth elements in FeS-rich eutrophic estuarine sediments receiving acid sulfate soil drainage. Chemical Geology, 308-309, 60-73. https://doi.org/10.1016/j.chemgeo.2012.03.012

Hebbali, A. (2018). Collinearity Diagnostics, Model Fit and Variable Contribution. Vignette for R Package 'olsrr'. Retrieved 2018.04.05, from https://cran.r-project.org/web/packages/olsrr/vignettes/regression_diagnostics.html.

Reimann, C., Filzmoser, P., Garrett, R.G., Dutter, R., (2008). Statistical Data Analysis Explained: Applied Environmental Statistics with R. John Wiley & Sons, Chichester, England (see Chapter 16).

CC-BY-SA • All content by Ratey-AtUWA. My employer does not necessarily know about or endorse the content of this website.
Created with rmarkdown in RStudio. Currently using the free yeti theme from Bootswatch.