Material to support teaching in Environmental Science at The University of Western Australia

Units ENVT3361, ENVT4461, and ENVT5503

Statistics for Comparisons

Parametric mean comparison tests

Comparisons pages: Parametric tests | Non-parametric tests

 

Activities for this session

1. Use a single-sided t- test to compare the mean of a variable with a fixed value (e.g. an environmental guideline)
2. Use a two -sided Welch's t-test to compare the means of 2 groups of a variable (i.e. categorised with a two-two-level factor)
3. Calculate a Cohen's d effect size for a 2-group mean comparison
4. Make a new factor using the cut() function in R or the Recode() function (in the car package)
5. Make relevant high-quality graphics to illustrate means comparisons: e.g. box plots with means, and plots-of-means [plotMeans()]
    
6. Repeat 1, 2, 3, & 5 above using analysis of variance (ANOVA) via the Welch's f test oneway.test(), to compare means for 3 or more groups
    
7. Generate a pairwise comparison of means from the analysis in step 6 (if there's time – we can leave this until the next session).

 

Code and Data

🔣 R code file for this workshop session

---

📊 Ashfield flats water data (afw19) in CSV format

📊 Smith's Lake / Veryard Reserve data (sv2017) in CSV format

 

Intro: Comparisons of means between groups

Comparison of means tests help you determine whether or not your groups of observations have similar means. The groups are defined by the value of a factor (a categorical variable) for each row (observation) of our dataset.

There are many cases in statistics where you'll want to compare means for two or more populations, samples, or sample types. The parametric tests like t-tests or ANOVA compare the variance between groups with the variance within groups, and use the relative sizes of these 2 variances to estimate the probability that means are different.

The parametric mean comparison tests require the variables to have normal distributions. We also often assume that all groups of observations have equal variance in the variable being compared. If the variances in each group are not similar enough (i.e. the variable is heteroskedastic), we need to modify or change the statistical test we use.

Means comparisons based on Null Hypothesis Statistical Testing (NHST) compare the variance between groups with the variance within groups, and generate a statistic which, if large/unlikely enough (i.e. p ≤ 0.05), allows rejection of the null hypothesis (H₀ = no difference between means in each/any groups).

In another session, we'll look at 'non-parametric' ways of comparing means, to be used when our variable(s) don't meet all of the requirements of conventional (parametric) statistical tests.

 

In this session we're going to use the 2017 Smith's Lake – Charles Veryard Reserves dataset (see Figure 1) to compare means between groups for factors having:

1. only two groups (using only the soil data);
2. more than two groups (using the whole dataset).

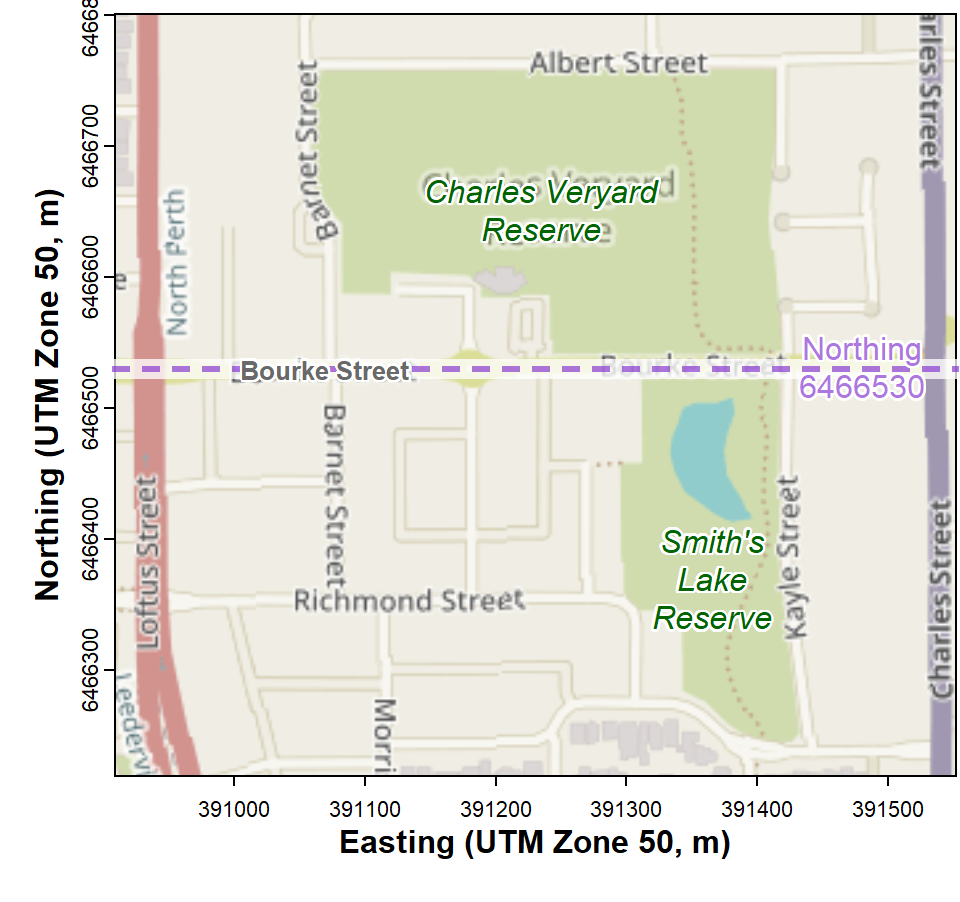
Figure 1: Map showing locations of the adjacent Charles Veryard Reserve and Smiths Lake Reserve, North Perth, Western Australia (these were the locations sampled for the sv2017 dataset).

 

Create a factor separating the two Reserves into groups AND limit the data to only soil

We split the dataset at Northing = 6466530 m, which represents Bourke Street.

require(car)
sv2017$Reserve <- cut(sv2017$Northing,
                      breaks = c(0,6466530,9999999),
                      labels = c("Smiths","Veryard"))
sv17_soil <- subset(sv2017, subset=sv2017$Type=="Soil")
cat("Number of soil samples in each reserve\n"); summary(sv17_soil$Reserve)

## Number of soil samples in each reserve

##  Smiths Veryard 
##      21      52

 

Check the newly-created factor with a plot

Note that:

• we include the option asp=1 in the plot function, so that distances are the same for the x- and y-coordinates
• the plot symbols, colours, and sizes are controlled by vectors of length 2: pch = c(1,2), col = c(2,4), and cex = c(1.25,1), followed by [Reserve] in square brackets, so that the value in each vector depends on the value of the factor Reserve for each sample (row).

par(mfrow=c(1,1), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.6,0.25,0),
    font.lab=2, font.main=3, cex.main=1, tcl=0.3)
with(sv17_soil, plot(Northing ~ Easting, asp=1,
     pch = c(1,2)[Reserve],
     col = c(2,4)[Reserve],
     cex = c(1.25,1)[Reserve],
     lwd = 2, xlab="Easting (UTM Zone 50, m)",
     ylab="Northing (UTM Zone 50, m)", cex.axis=0.85, cex.lab=0.9,
     main = "Samples by reserve"))
abline(h = 6466530, lty=2, col="gray")
legend("bottomleft", legend = c("Smiths Lake","Charles Veryard"),
       cex = 1, pch = c(1,2), col = c(2,4),
       pt.lwd = 2, pt.cex = c(1.25, 1), title = "Reserve",
       bty = "n", inset = 0.02)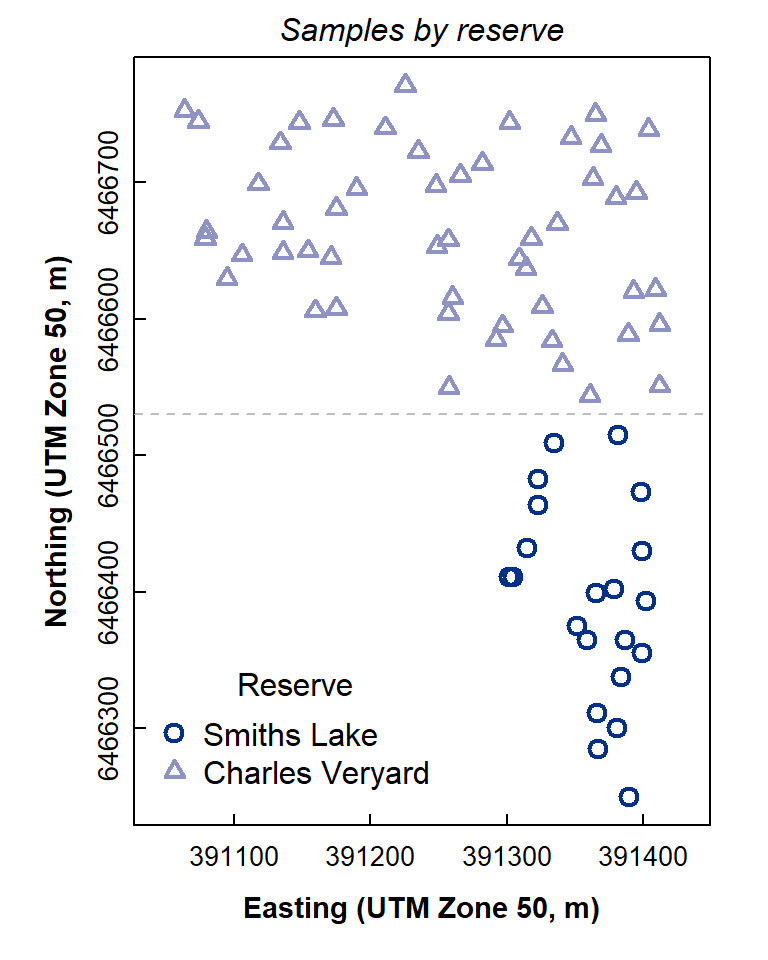

Figure 2: Map-style plot showing locations of soil samples at Charles Veryard and Smiths Lake Reserves.

The plot in Figure 2 looks OK! You may have just made your first R map!

We can also draw the plot using the ggplot2 package (make sure to include coord-equal() to preserve a map-like aspect ratio):

library(ggplot2)
ggplot(sv17_soil, aes(x=Easting, y=Northing, shape=Reserve, color=Reserve)) +
  geom_point(size=2) + coord_equal() +
  scale_colour_manual(values=c("darkgreen","olivedrab"))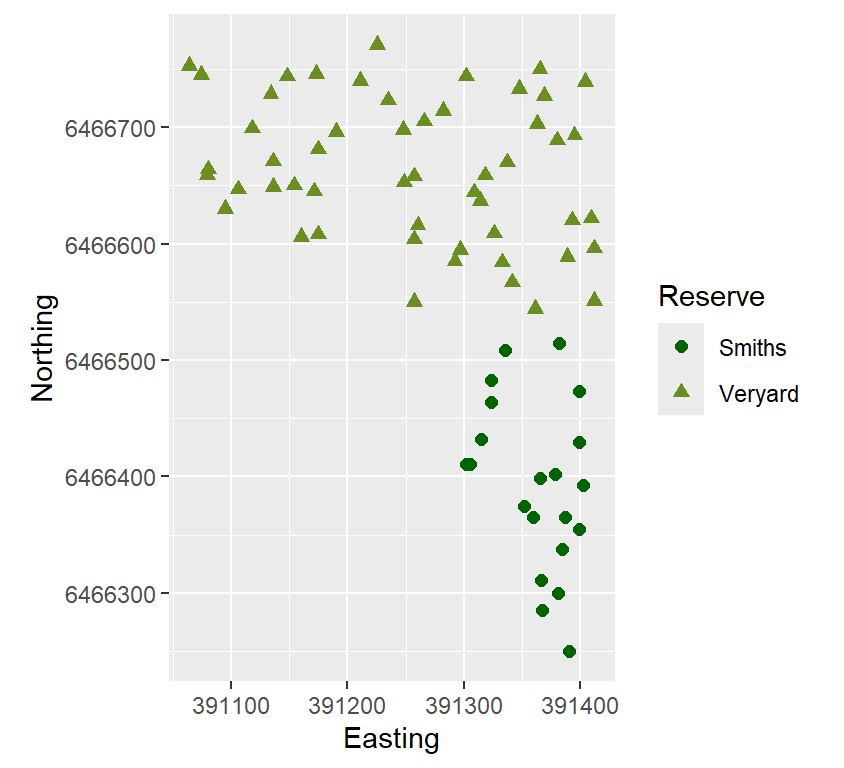

Figure 3: Map-like scatterplot made with ggplot, showing locations of soil samples at Charles Veryard and Smiths Lake Reserves.

---

"...we have our work to do
Just think about the average..."

--- Rush, from the song 2112 (The Temples of Syrinx)

---

 

Means comparisons for exactly two groups

For variables which are normally distributed, we can use conventional, parametric statistics. The following example applies a t-test to compare mean values between Reserve. By default the R function t.test() uses the Welch t-test, which doesn't require the variance in each group to be equal (i.e., the Welch t-test is OK for heteroskedastic variables, but we should check anyway!).
Of course, we still need to use appropriately transformed variables!

Homogeneity of variance using the variance ratio test or Bartlett's Test

We can actually check if the variances are equal in each group using Bartlett's Test (bartlett.test()), or for this example with exactly two groups we can use the var.test() function (do they both give the same conclusion?):

require(car)
powerTransform(sv17_soil$Na)
sv17_soil$Na.pow <- (sv17_soil$Na)^0.127 # from results of powerTransform()

with(sv17_soil, shapiro.test(Na.pow))
with(sv17_soil, var.test(Na.pow ~ Reserve))
with(sv17_soil, bartlett.test(Na.pow ~ Reserve))

## Estimated transformation parameter 
## sv17_soil$Na 
##    0.1266407 
## 
##  Shapiro-Wilk normality test
## 
## data:  Na.pow
## W = 0.99135, p-value = 0.9222
## 
## 
##  F test to compare two variances
## 
## data:  Na.pow by Reserve
## F = 1.664, num df = 15, denom df = 51, p-value = 0.1789
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.7911095 4.2363994
## sample estimates:
## ratio of variances 
##           1.663991 
## 
## 
##  Bartlett test of homogeneity of variances
## 
## data:  Na.pow by Reserve
## Bartlett's K-squared = 1.6001, df = 1, p-value = 0.2059

Both the variance-ratio and Bartlett tests show that H₀ (that variances are equal) can not be rejected. We can visualise this with (for instance) a boxplot or density plot (Figure 4; we need the car package for the densityPlot() function):

require(car)
par(mfrow=c(1,2), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.6,0.5,0),
    font.lab=2, font.main=3, cex.main=0.8, tcl=-0.2,
    cex.lab = 1, cex.axis = 1)
stripchart(sv17_soil$Na.pow ~ sv17_soil$Reserve, vertical=TRUE, method="jitter",
           pch=15, cex=1.3, col=c("#00008080","#a0600080"),
        xlab="Reserve", ylab="Na (power-transformed)")
mtext("(a)", 3, -1.3, adj=0.05, cex=1.2)
densityPlot(Na.pow ~ Reserve, data=sv17_soil, adjust=1.5, ylim=c(0,5), 
            xlab="Na (power transformed)", col=c("#000080","#a06000"))
mtext("(b)", 3, -1.3, adj=0.05, cex=1.2)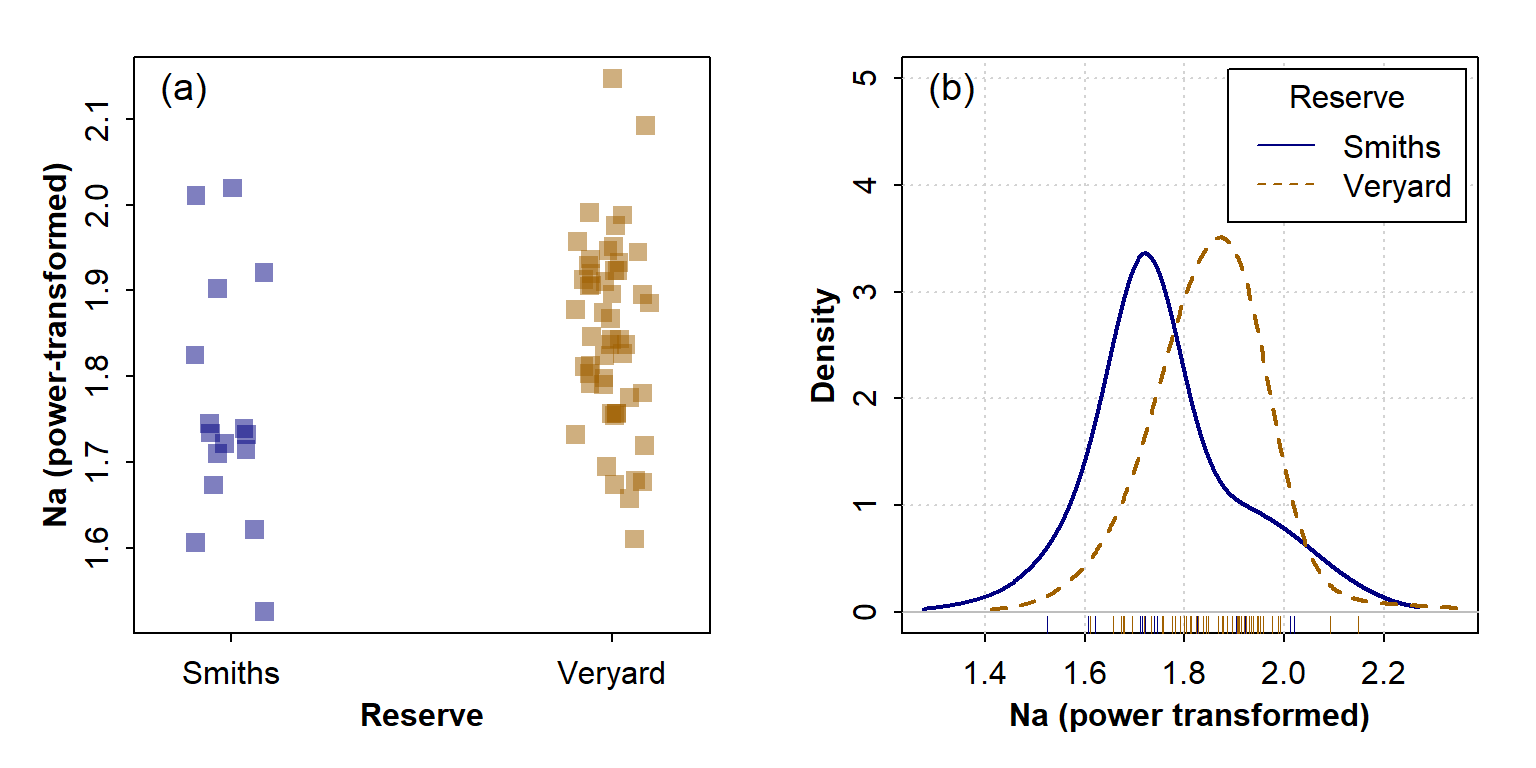

Figure 4: Graphical visulaization of variance (the 'spread' of the distribution) in each group using (a) a strip chart and (b) a density plot.

In each case it's apparent that the variance in Na in the Veryard soil is similar to that at Smith's Lake, illustrating the conclusion from the statistical tests.

 

The power term from powerTransform() is ≃ 0.127, so we make a new power-transformed column Na.pow using this value. The shapiro.test() shows that Na.pow is normally distributed, and var.test() shows that the variances are approximately equal, as do the boxplot and density plot. So we can apply the t.test() with the option var.equal=TRUE (i.e. a 'standard' two-sample t-test).

t.test(sv17_soil$Na.pow ~ sv17_soil$Reserve, var.equal=TRUE)

## 
##  Two Sample t-test
## 
## data:  sv17_soil$Na.pow by sv17_soil$Reserve
## t = -2.6175, df = 66, p-value = 0.01097
## alternative hypothesis: true difference in means between group Smiths and group Veryard is not equal to 0
## 95 percent confidence interval:
##  -0.15360517 -0.02067153
## sample estimates:
##  mean in group Smiths mean in group Veryard 
##              1.762519              1.849657

We can visualize means comparisons in a few different ways – see Figure 5. My favourite is the boxplot with means included as extra information - with a bit of additional coding we can include the 95% confidence intervals as well! (but this is not shown in this document).

 

Visualising differences in means - 2 groups

par(mfrow=c(1,2), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.7,0.3,0),
    font.lab=2, font.main=3, cex.main=1, tcl=0.3)
boxplot(sv17_soil$Na.pow ~ sv17_soil$Reserve, 
        notch=F, col="gainsboro",
        xlab="Reserve", ylab="Na (power-transformed)")
mtext("(a)", 3, -1.25, adj=0.05, font=2)
#
# the second plot is a box plot with the means overplotted
boxplot(sv17_soil$Na.pow ~ sv17_soil$Reserve, 
        notch=F, col="bisque", ylim=c(1.4,2.2),
        xlab="Reserve", ylab="Na (power-transformed)")
# make a temporary object 'meanz' containing the means
meanz <- tapply(sv17_soil$Na.pow, sv17_soil$Reserve, mean, na.rm=T)
# plot means as points (boxplot boxes are centered on whole numbers)
points(seq(1, nlevels(sv17_soil$Reserve)), meanz, 
       col = "royalblue", pch = 3, lwd = 2)
legend("bottomright", "Mean values", 
       pch = 3, pt.lwd = 2, col = "royalblue",
       bty = "n", inset = 0.01)
mtext("(b)", 3, -1.25, adj=0.05, font=2)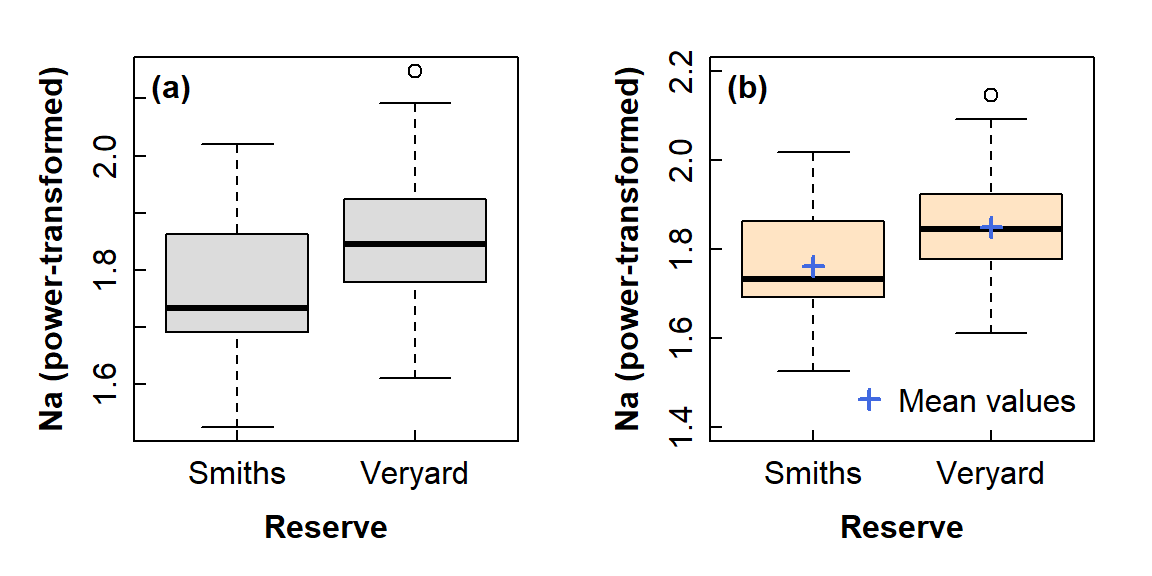

Figure 5: Graphical comparison of means between groups using: (a) a standard box plot; (b) a box plot also showing mean values in each group. You would not include both options in a report!

rm(meanz) # tidy up

[skip to Figure 8 for a 3-group comparison]

 

The ggplot connoisseurs can also draw such a boxplot (Figure 6):

# there's probably a more efficient way to do this in ggplot!
meanz <- data.frame(x1=levels(sv17_soil$Reserve),
                    y1=tapply(sv17_soil$Na.pow, sv17_soil$Reserve, mean, na.rm=T),
                    x2=rep("Mean",2))
shapes <- c("Mean" = 3, "Outliers" = 1)
ggplot(sv17_soil, aes(x=Reserve, y=Na.pow)) +
  labs(y="Na (power-transformed)") +
  geom_boxplot(fill="mistyrose", outlier.shape=1) + theme_bw() +
  geom_point(data = meanz, aes(x=x1, y=y1, shape=x2), size=2, 
             stroke=1.2, col="firebrick") +
  scale_shape_manual(name="Legend", values=3) +
  theme(axis.title = element_text(face="bold"))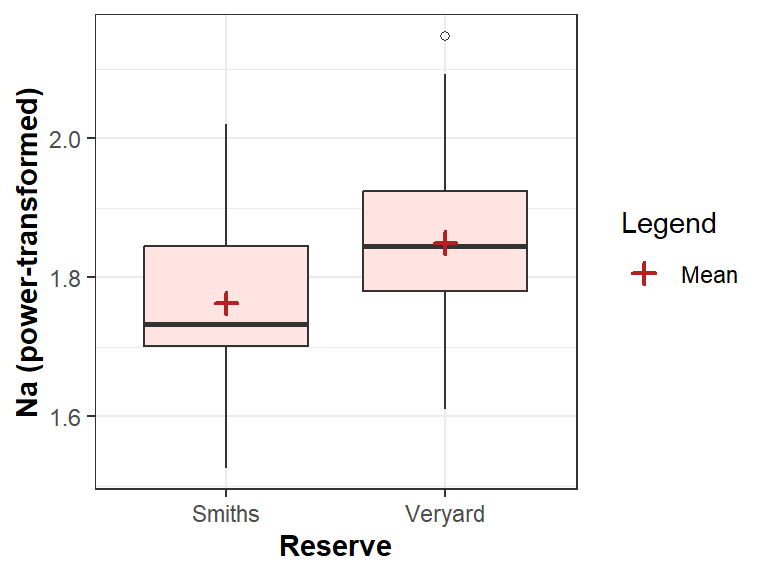

Figure 6 Boxplot for 2-group comparison, showing means, and drawn with ggplot2.

 

Effect size for means comparisons: Cohens d

Statistical tests which compare means only estimate if there is a difference or not. We would also usually like to know how big the difference (or 'effect') is! The Cohen's d statistic is a standardised measure of effect size available in the effsizeh R package.

require(effsize)
cohen.d(sv17_soil$Na.pow ~ sv17_soil$Reserve)

## 
## Cohen's d
## 
## d estimate: -0.7483083 (medium)
## 95 percent confidence interval:
##      lower      upper 
## -1.3332988 -0.1633178

The calculated value of Cohen's d is 0.5 ≤ d < 0.8, which is medium. The 95% CI for the estimate of Cohen's d (i.e. between lower and upper) does not include zero, so we can probably rely on it.

More recently than Cohen, Sawilowsky (2009) proposed that for Cohen's d:

0.01 ≤	d	< 0.2	very small
0.2 ≤	d	< 0.5	small
0.5 ≤	d	< 0.8	medium
0.8 ≤	d	< 1.2	large
1.2 ≤	d	< 2.0	very large
	d	> 2.0	huge

 

Means comparisons for 3 or more groups

If we have a factor with 3 or more levels (a.k.a. groups, or categories), we can use analysis of variance (ANOVA) to compare means of a normally distributed variable. In this example we'll use the factor Type (= sample type) from the complete 2017 Smith's – Veryard data (not just soil!).
We still need to use appropriately transformed variables, and we need to know if group variances are equal!

Check homogeneity of variances, 3 or more groups

ANOVA also requires variance for each group to be (approximately) equal. Since there are more than 2 groups, we need to use the Bartlett test.

shapiro.test(sv2017$Ca.pow)
bartlett.test(sv2017$Ca.pow ~ sv2017$Type)

## 
##  Shapiro-Wilk normality test
## 
## data:  sv2017$Ca.pow
## W = 0.97634, p-value = 0.1073
## 
## 
##  Bartlett test of homogeneity of variances
## 
## data:  sv2017$Ca.pow by sv2017$Type
## Bartlett's K-squared = 8.9659, df = 2, p-value = 0.0113

The shapiro.test() p-value is > 0.05, so we can accept H₀ that Ca.pow is normally distributed. In contrast, the bartlett.test() p-value is ≤ 0.05, so we reject H₀ of equal variances (i.e. Ca.pow is heteroscedastic).

require(car)
par(mfrow=c(1,2), mar=c(3,3,0.5,0.5), mgp=c(1.6,0.5,0),
    font.lab=2, font.main=3, cex.main=0.8, tcl=-0.2,
    cex.lab = 1, cex.axis = 1)
stripchart(sv2017$Ca.pow ~ sv2017$Type, method="jitter", 
        pch=15, cex=1.3, vertical=T, col=plasma(3, alpha=0.5, end=0.5),
        xlab="Reserve", ylab="Ca (power-transformed)")
mtext("(a)", 3, -1.3, adj=0.95)
densityPlot(sv2017$Ca.pow ~ sv2017$Type, adjust=2, xlim=c(-0.1,0.6), ylim=c(0,16), 
            xlab="Ca (power transformed)", legend=list(title="Type"), 
            col=plasma(3, end=0.5)) ; mtext("(a)", 3, -1.3, adj=0.95)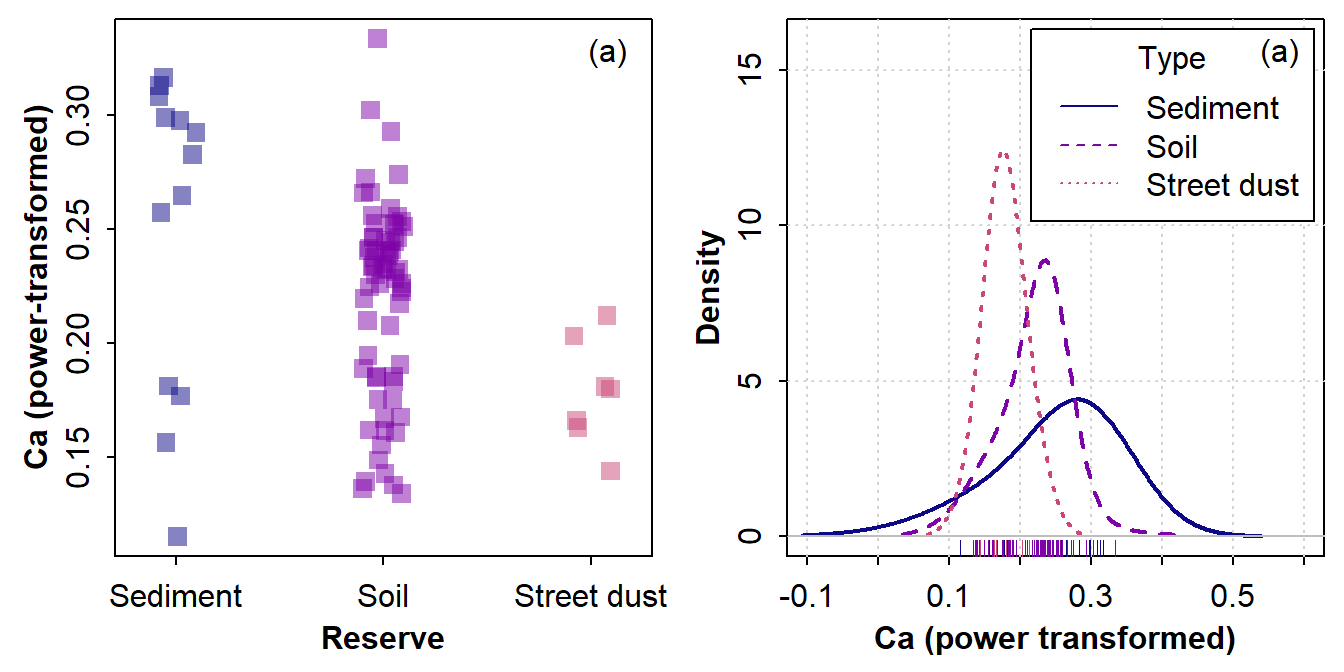

Figure 7: Graphical visualization of variance (the spread of the distribution) in 3 groups using (a) a strip chart and (b) a density plot.

In each case it seems that the variance in power-transformed Ca is Sediment > Soil > Street dust (Figure 7). We can check the actual variance values using tapply(), and this confirms our interpretation:

cat("--- Variances for each factor level ---\n")
with(sv2017, tapply(Ca.pow, Type, var, na.rm=TRUE))

## --- Variances for each factor level ---
##     Sediment         Soil  Street dust 
## 0.0047080391 0.0018348117 0.0005551313

 

We now know that we can use a parametric test (based on Ca.pow being normally distributed) which corrects for unequal variance (since we found that Ca.pow is heteroscedastic).

oneway.test(sv2017$Ca.pow ~ sv2017$Type, var.equal = FALSE)
cat("\nMeans for transformed variable\n");
meansAl <- tapply(sv2017$Ca.pow, sv2017$Type, mean, na.rm=TRUE);
print(signif(meansAl,3)) # output means with appropriate significant digits
cat("\nMeans for original (untransformed) variable\n");
meansCa <- tapply(sv2017$Ca, sv2017$Type, mean, na.rm=TRUE);
print(signif(meansAl,4)) # output means with appropriate significant digits
rm(meansCa) # tidy up

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  sv2017$Ca.pow and sv2017$Type
## F = 10.016, num df = 2.000, denom df = 15.485, p-value = 0.001617
## 
## 
## Means for transformed variable
##    Sediment        Soil Street dust 
##       0.251       0.220       0.178 
## 
## Means for original (untransformed) variable
##    Sediment        Soil Street dust 
##      0.2509      0.2203      0.1785

In the output above, the p-value from our oneway.test() is less than 0.05 based on the large value for the F statistic. This allows us to reject the null hypothesis of equal means. As for a two-group comparison, we can visualize the differences in means in different ways (Figure @ref(fig:meancomp-plots-3groups))

 

Visualising differences in means - 3 or more groups

par(mfrow=c(1,2), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.7,0.3,0),
    font.lab=2, font.main=3, cex.main=1, tcl=0.2,
    cex.axis=0.9, lend = "square", ljoin = "mitre")
boxplot(sv2017$Ca.pow ~ sv2017$Type, notch=TRUE, 
        cex = 1.2, col="grey92", ylim=c(0.08,0.35), 
        xlab="Sample type", ylab="Ca (power-transformed)")
mtext("(a)", 3, -1.5, adj=0.97, font=2) # label each sub-plot
boxplot(sv2017$Ca.pow ~ sv2017$Type, notch=F, 
        col=c("cadetblue","moccasin","thistle"), 
        cex = 1.2, ylim=c(0.08,0.35), 
        xlab="Reserve", ylab="Ca (power-transformed)")
mtext("(b)", 3, -1.5, adj=0.97, font=2) # label each sub-plot
meanz <- tapply(sv2017$Ca.pow, sv2017$Type, mean, na.rm=T)
points(seq(1, nlevels(sv2017$Type)), meanz, 
       col = "white", pch = 3, lwd = 4, cex = 1.3)
points(seq(1, nlevels(sv2017$Type)), meanz, 
       col = "firebrick", pch = 3, lwd = 2, cex = 1.2)
legend("bottomright", legend="Mean values", cex=0.9, y.int=0.2, 
       pch = 3, pt.lwd = 2, col = "firebrick", pt.cex = 1.2,
       bty = "o", inset = 0.03, box.col="#00000000", bg="#d0d0d040")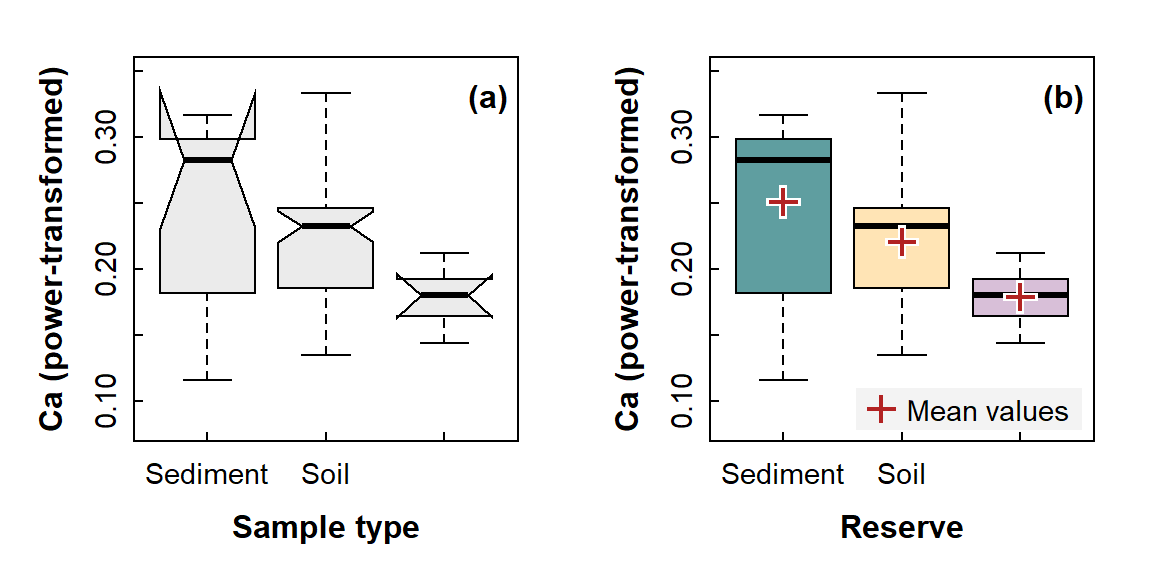

Figure 8: Graphical comparisons of means between 3 or more groups: (a) a notched box plot (notches are approximate 95% confidence intervals around the median); (b) a box plot also showing mean values in each group. You would not include both options in a report!

rm(meanz) # tidy up

Look back at Figure 5. Why is Figure 8 better? (Hint: it's not the notches in Figure 8a – these are larger than the interquartile range boxes for 2 groups, so they look kind of weird. If this happens, it's best to leave them out using notch=FALSE.)

 

Visualising 3-group differences with ggplot2

# there's probably a more efficient way to do this in ggplot!
meanz <- data.frame(x1=levels(sv2017$Type),
                    y1=tapply(sv2017$Ca.pow, sv2017$Type, mean, na.rm=T),
                    x2=rep("Mean",nlevels(sv2017$Type)))
ggplot(sv2017, aes(x=Type, y=Ca.pow)) +
  labs(y="Ca (power-transformed)") +
  geom_boxplot(fill="papayawhip", outlier.shape=1) + theme_bw() +
  geom_point(data = meanz, aes(x=x1, y=y1, shape=x2), size=2.2, 
             stroke=0.8, col="slateblue") +
  scale_shape_manual(name="Key", values=10) +
  theme(axis.title = element_text(face="bold"))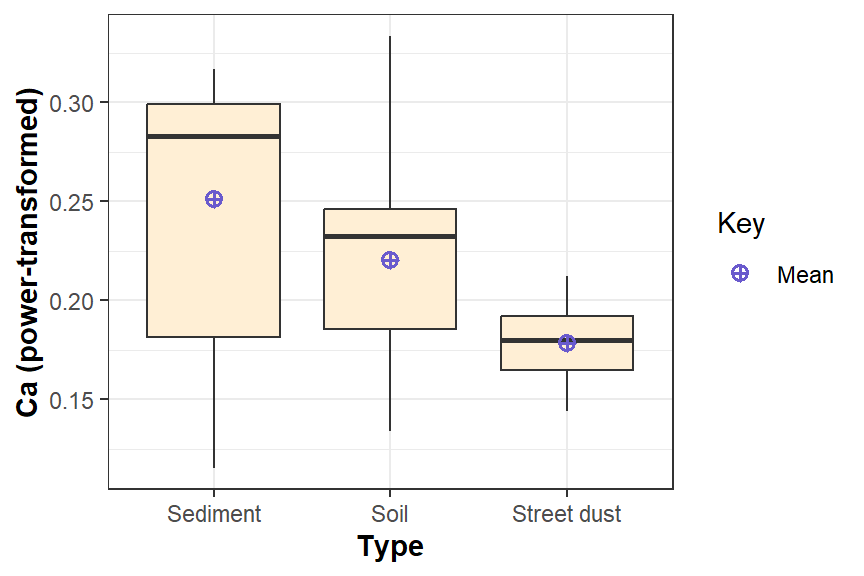

Figure 9: Boxplot for 3-group comparison, showing means, and drawn with ggplot2.

---

"The analysis of variance is not a mathematical theorem, but rather a convenient method of arranging the arithmetic."

--- Ronald Fisher, the developer of ANOVA

---

 

Effect sizes for 3 or more groups

It's not possible to calculate Effect sizes for 3 or more groups directly. We would need to create subsets of our dataset which include only two groups** (e.g., with only Soil and Sediment), and then run cohen.d() from the 'effsize' R package. Or we could do some custom coding...

 

Pairwise comparisons

If our analysis of variance allows rejection of H₀, we still don't necessarily know which means are different. The test may return a p-value ≤ 0.05 even if only one mean is different from all the others. If the p-value ≤ 0.05, we can compute Pairwise Comparisons (there's no point if the 'overall' p-value from the initial test is > 0.05). The examples below show pairwise comparisons in an analysis of variance for Ba, in groups defined by the factor Type.

The most straightforward way to conduct pairwise comparisons is with the pairwise.t.test() function – this is what we recommend. We can generate the convenient 'compact letter display' using the R packages rcompanion and multcompView. With the compact letter display, factor levels (categories) having the same letter are not significantly different (pairwise p > 0.05).

Note that pairwise comparisons [should] always adjust p-values to greater values, to account for the increased likelihood of Type 1 Error (false positives) with multiple comparisons. There are several ways of making this correction, such as Holm's method.

First, we know we can apply a post-hoc pairwise test, since the overall effect of Type on Ba is significant (p ≈ 0.002):

with(sv2017, shapiro.test(Ba.log))
with(sv2017, bartlett.test(Ba.log ~ Type))
with(sv2017, oneway.test(Ba.log ~ Type, var.equal = TRUE))

## 
##  Shapiro-Wilk normality test
## 
## data:  Ba.log
## W = 0.9885, p-value = 0.6358
## 
## 
##  Bartlett test of homogeneity of variances
## 
## data:  Ba.log by Type
## Bartlett's K-squared = 3.4694, df = 2, p-value = 0.1765
## 
## 
##  One-way analysis of means
## 
## data:  Ba.log and Type
## F = 6.6595, num df = 2, denom df = 85, p-value = 0.002057

How did we get Ba.log? (You need to calculate it yourself with a line of R code!). Also, what do the Shapiro-Wilk and Bartlett tests tell us about our choice of means comparison test?

Next we generate the compact letters using the fullPTable() function from the rcompanion package and multcompLetters() from the multcompView package as below. Note that since Ba.log has equal variance across Type groups (see above), we can use the default pairwise.t.test() options. If Ba.log was heteroscedastic, we would have used pairwise.t.test(Ba.log, Type, pool.sd = FALSE) instead.

library(rcompanion)
library(multcompView)
(pwBa <- with(sv2017, pairwise.t.test(Ba.log, Type)))
cat("\n==== Compact letters ====\n") 
pwBa_pv <- fullPTable(pwBa$p.value)                 # from rcompanion
multcompLetters(pwBa_pv)                            # from multcompView

## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  Ba.log and Type 
## 
##             Sediment Soil  
## Soil        0.0031   -     
## Street dust 0.0078   0.3634
## 
## P value adjustment method: holm 
## 
## ==== Compact letters ====
##    Sediment        Soil Street dust 
##         "a"         "b"         "b"

In the output above, the table of p-values shows a significant difference (p < 0.05) between Sediment and Soil, and Sediment and Street dust (note the use of Holm's p-value adjustment, which is the default method). We get the same interpretation from the compact letters; Sediment ("a") is different from Soil and Street dust (both "b"). Since Soil and Street dust have the same letter ("b"), they are not significantly different, which matches the p-value (0.3634).

 

OPTIONAL: Pairwise compact letters alternative

This method using the cld() function is way harder to make sense of... it's probably more rigorous, but leads to the same conclusion. We need to load the multcomp package.

anovaBa <- aov(Ba.log ~ Type, data=sv2017)
require(multcomp)
pwise0 <- glht(anovaBa, linfct = mcp(Type="Tukey")) # anovaBa from above
cld(pwise0)

##    Sediment        Soil Street dust 
##         "a"         "b"         "b"

Groups assigned a different letter are significantly different at the specified probability level (p ≤ 0.05 by default). In this example, Ba concentration in sediment (a) is significantly different from both Soil and Street dust (both b, so not different from each other).

We can get the confidence intervals and p-values for each pairwise comparison using the TukeyHSD() function (HSD='Honestly Significant Difference'):

 

OPTIONAL: Pairwise Tukey multiple comparisons of means

Also more complicated to understand and, like the code above, we need to have a normally-distributed, homoscedastic, variable. Usually we don't.

TukeyHSD(anovaBa)

rm(list=c("anovaBa","pwise0"))    # tidy up

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = Ba.log ~ Type, data = sv2017)
## 
## $Type
##                            diff         lwr       upr     p adj
## Soil-Sediment        0.20660696  0.06143156 0.3517824 0.0029746
## Street dust-Sediment 0.27953479  0.05469616 0.5043734 0.0108295
## Street dust-Soil     0.07292783 -0.11744448 0.2633002 0.6331075

The table of output from TukeyHSD() (after $Type) shows the differences between mean values for each pairwise comparison (diff), and the lower (lwr) and upper (upr) limits of the 95% confidence interval for the difference in means. If the 95% CI includes zero (e.g. for the Street dust-Soil comparison above), there is no significant difference.

This conclusion is supported by the last column of output, showing an adjusted p-value of 0.633 (i.e. > 0.05) for the Street dust-Soil comparison. Also, as indicated by the 'compact letter display' from cld() above, any comparison including Sediment has p ≤ 0.05.

References and R Packages

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). New York:Academic Press.

Sawilowsky, S.S. (2009). New Effect Size Rules of Thumb. Journal of Modern Applied Statistical Methods 8:597-599.

Run the R code below to get citation information for the R packages used in this document.

citation("car", auto = TRUE)
citation("ggplot2", auto = TRUE)
citation("effsize", auto = TRUE)
citation("multcomp", auto = TRUE)
citation("rcompanion", auto = TRUE)
citation("multcompView", auto = TRUE)

## To cite package 'car' in publications use:
## 
##   Fox J, Weisberg S, Price B (2023). _car: Companion to Applied Regression_. R package
##   version 3.1-2, <https://CRAN.R-project.org/package=car>.
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {car: Companion to Applied Regression},
##     author = {John Fox and Sanford Weisberg and Brad Price},
##     year = {2023},
##     note = {R package version 3.1-2},
##     url = {https://CRAN.R-project.org/package=car},
##   }
## To cite package 'ggplot2' in publications use:
## 
##   Wickham H, Chang W, Henry L, Pedersen T, Takahashi K, Wilke C, Woo K, Yutani H,
##   Dunnington D, van den Brand T (2024). _ggplot2: Create Elegant Data Visualisations
##   Using the Grammar of Graphics_. R package version 3.5.1,
##   <https://CRAN.R-project.org/package=ggplot2>.
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {ggplot2: Create Elegant Data Visualisations Using the Grammar of Graphics},
##     author = {Hadley Wickham and Winston Chang and Lionel Henry and Thomas Lin Pedersen and Kohske Takahashi and Claus Wilke and Kara Woo and Hiroaki Yutani and Dewey Dunnington and Teun {van den Brand}},
##     year = {2024},
##     note = {R package version 3.5.1},
##     url = {https://CRAN.R-project.org/package=ggplot2},
##   }
## To cite package 'effsize' in publications use:
## 
##   Torchiano M (2020). _effsize: Efficient Effect Size Computation_. R package version
##   0.8.1, <https://CRAN.R-project.org/package=effsize>.
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {effsize: Efficient Effect Size Computation},
##     author = {Marco Torchiano},
##     year = {2020},
##     note = {R package version 0.8.1},
##     url = {https://CRAN.R-project.org/package=effsize},
##   }
## To cite package 'multcomp' in publications use:
## 
##   Hothorn T, Bretz F, Westfall P (2023). _multcomp: Simultaneous Inference in General
##   Parametric Models_. R package version 1.4-25,
##   <https://CRAN.R-project.org/package=multcomp>.
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {multcomp: Simultaneous Inference in General Parametric Models},
##     author = {Torsten Hothorn and Frank Bretz and Peter Westfall},
##     year = {2023},
##     note = {R package version 1.4-25},
##     url = {https://CRAN.R-project.org/package=multcomp},
##   }
## To cite package 'rcompanion' in publications use:
## 
##   Mangiafico S (2024). _rcompanion: Functions to Support Extension Education Program
##   Evaluation_. R package version 2.4.36,
##   <https://CRAN.R-project.org/package=rcompanion>.
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {rcompanion: Functions to Support Extension Education Program Evaluation},
##     author = {Salvatore Mangiafico},
##     year = {2024},
##     note = {R package version 2.4.36},
##     url = {https://CRAN.R-project.org/package=rcompanion},
##   }
## To cite package 'multcompView' in publications use:
## 
##   Graves S, Piepho H, Dorai-Raj LSwhfS (2024). _multcompView: Visualizations of Paired
##   Comparisons_. R package version 0.1-10,
##   <https://CRAN.R-project.org/package=multcompView>.
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {multcompView: Visualizations of Paired Comparisons},
##     author = {Spencer Graves and Hans-Peter Piepho and Luciano Selzer with help from Sundar Dorai-Raj},
##     year = {2024},
##     note = {R package version 0.1-10},
##     url = {https://CRAN.R-project.org/package=multcompView},
##   }
## 
## ATTENTION: This citation information has been auto-generated from the package
## DESCRIPTION file and may need manual editing, see 'help("citation")'.

 

---

CC-BY-SA • All content by Ratey-AtUWA. My employer does not necessarily know about or endorse the content of this website.
Created with rmarkdown in RStudio. Currently using the free yeti theme from Bootswatch.