UWA logoMaterial to support teaching in Environmental Science at The University of Western Australia

Units ENVT3361, ENVT4461, and ENVT5503

Relationships pages: Correlations | Simple linear regression | Grouped linear regression | Multiple linear regression

 

Suggested activities

Using the R code file provided and the sv2017 dataset:

If you need to install packages like car or psych this should be done first, either:

  1. from the RStudio packages tab;
  2. running some code like the example below for each package you need to install.
        install.packages("psych")

 

Basic correlation analyses

# load packages we need
library(car)        # for various plotting and regression-specific functions
library(viridis)    # colour palettes for improved graph readability
library(psych)      # utility functions
library(RcmdrMisc)  # utility functions
library(corrplot)   # plotting of correlation heatmaps

Let's look at the relationship between Cd and Zn in the Smiths Lake and Charles Veryard Reserves data from 2017.
For Pearson's correlation we need variables with normal distributions, so first log10-transform Cd and Zn...

git <- "https://raw.githubusercontent.com/Ratey-AtUWA/Learn-R-web/main/"
sv2017 <- read.csv(paste0(git,"sv2017_original.csv"), stringsAsFactors = TRUE)
sv2017$Cd.log <- log10(sv2017$Cd)
sv2017$Zn.log <- log10(sv2017$Zn)

...and test if the distributions are normal. Remember that the null hypothesis for the Shapiro-Wilk test is that "the distribution of the variable of interest is not different from a normal distribution". So, if the P-value ≥ 0.05, we can't reject the null and therefore our variable is normally distributed.

shapiro.test(sv2017$Cd)
shapiro.test(sv2017$Cd.log)
shapiro.test(sv2017$Zn)
shapiro.test(sv2017$Zn.log)
## 
##  Shapiro-Wilk normality test
## 
## data:  sv2017$Cd
## W = 0.63001, p-value = 1.528e-12
## 
## 
##  Shapiro-Wilk normality test
## 
## data:  sv2017$Cd.log
## W = 0.97272, p-value = 0.1006
## 
## 
##  Shapiro-Wilk normality test
## 
## data:  sv2017$Zn
## W = 0.6155, p-value = 7.75e-14
## 
## 
##  Shapiro-Wilk normality test
## 
## data:  sv2017$Zn.log
## W = 0.9828, p-value = 0.295

 

Pearson's r changes with transformation

cor.test(sv2017$Cd, sv2017$Zn, alternative="two.sided", 
         method="pearson") # is Pearson valid?
cor.test(sv2017$Cd.log, sv2017$Zn.log, alternative="two.sided", 
         method="pearson") # is Pearson valid?
## 
##  Pearson's product-moment correlation
## 
## data:  sv2017$Cd and sv2017$Zn
## t = 9.8415, df = 74, p-value = 4.357e-15
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.6353031 0.8363947
## sample estimates:
##       cor 
## 0.7529165 
## 
## 
##  Pearson's product-moment correlation
## 
## data:  sv2017$Cd.log and sv2017$Zn.log
## t = 7.696, df = 74, p-value = 4.859e-11
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.5193717 0.7756160
## sample estimates:
##       cor 
## 0.6667536

For the Pearson correlation we get a t statistic and associated degrees of freedom (df), for which there is a p-value. The null hypothesis is that there is "no relationship between the two variables", which we can reject if p ≤ 0.05. We also get a 95% confidence interval for the correlation coefficient, and finally an estimate of Pearson's r (cor).

A Spearman coefficient doesn't change with transformation, since it is calculated from the ranks (ordering) of each variable.

cor.test(sv2017$Cd, sv2017$Zn, alternative="two.sided", 
         method="spearman") # can we use method="pearson"?
cor.test(sv2017$Cd.log, sv2017$Zn.log, alternative="two.sided", 
         method="spearman") # can we use method="pearson"?
## 
##  Spearman's rank correlation rho
## 
## data:  sv2017$Cd and sv2017$Zn
## S = 25750, p-value = 2.494e-10
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.6479832 
## 
## 
##  Spearman's rank correlation rho
## 
## data:  sv2017$Cd.log and sv2017$Zn.log
## S = 25750, p-value = 2.494e-10
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.6479832

For the Spearman correlation we get an S statistic and associated p-value. The null hypothesis is that there is no relationship between the two variables, which we can reject if p ≤ 0.05. We also get an estimate of Spearman's rho (analogous to Pearson's r).

 

Simple scatterplot by groups

We're using base R to plot - you might like to try using scatterplot() from the car package or the ggplot2 package.

Before plotting, we first set our desired colour palette (optional) and graphics parameters (optional, but useful and recommended!). We end up with the plot in Figure 1 which helps us interpret the correlation coefficient.

palette(c("black",viridis::plasma(8)[2:7],"white"))
par(mfrow=c(1,1), mar=c(3,3,1,1), mgp=c(1.5,0.3,0), oma=c(0,0,0,0), tcl=0.2,
    lend="square", ljoin="mitre", font.lab=2)

# . . . then plot the data
with(sv2017, plot(Cd~Zn, col=c(5,3,1)[Type], log="xy", 
     pch=c(16,1,15)[Type], lwd=c(1,2,1)[Type], 
     cex=c(1.2,1,1)[Type], xlab="Zn (mg/kg)", ylab="Cd (mg/kg)"))
abline(lm(sv2017$Cd.log~sv2017$Zn.log)) # line of best fit using lm() function
legend("topleft", legend=c(levels(sv2017$Type),"Best-fit line ignoring Type"), 
       col=c(5,3,1,1), pch=c(16,1,15,NA), pt.lwd=c(1,2,1), lwd = c(NA,NA,NA,1), 
       pt.cex=c(1.2,1,1), bty="n", y.intersp = 0.75,
       title=expression(italic("Sample Type")))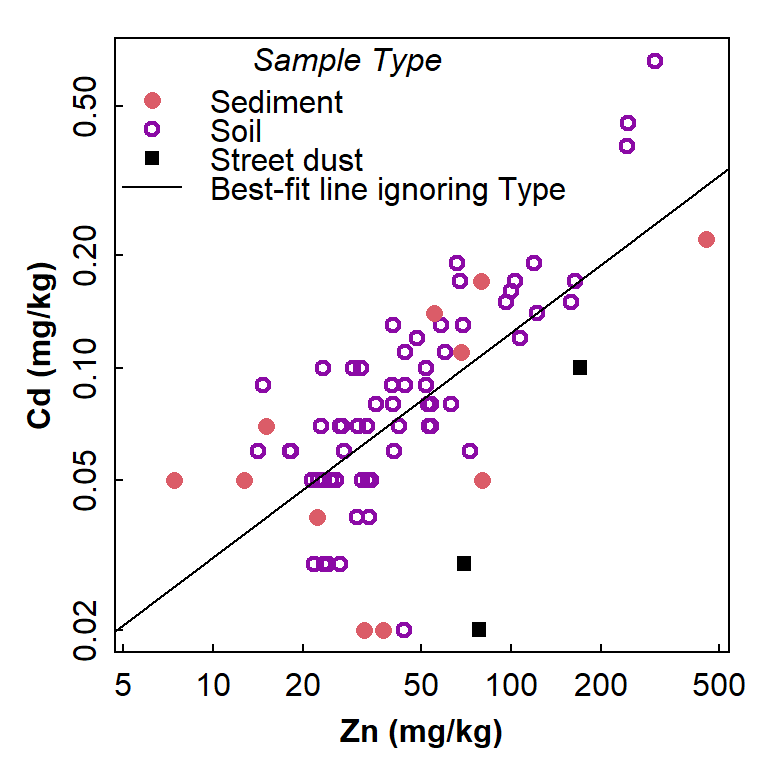
Figure 1: Scatterplot showing the relationship between Cd and Zn, with observations identified by Type but showing the regression line for all data independent of grouping.

Figure 1: Scatterplot showing the relationship between Cd and Zn, with observations identified by Type but showing the regression line for all data independent of grouping.

 

"The invalid assumption that correlation implies cause is probably among the two or three most serious and common errors of human reasoning."

--- Stephen Jay Gould

Correlation matrix

We'll generate Spearman correlation matrices in these examples, but it's easy to change the code to generate Pearson (or other) correlation matrices.
The p-values give the probability of the observed relationship if the null hypothesis (i.e. no relationship) is true.

library(psych) # needed for corTest() function
corr_table <- corTest(sv2017[c("pH","Al","Ca","Fe","Cd","Pb","Zn")], 
                    method="spearman")
print(corr_table)
## Call:corTest(x = sv2017[c("pH", "Al", "Ca", "Fe", "Cd", "Pb", "Zn")], 
##     method = "spearman")
## Correlation matrix 
##      pH   Al   Ca   Fe   Cd   Pb   Zn
## pH 1.00 0.31 0.68 0.29 0.23 0.13 0.12
## Al 0.31 1.00 0.32 0.45 0.19 0.07 0.16
## Ca 0.68 0.32 1.00 0.42 0.25 0.21 0.35
## Fe 0.29 0.45 0.42 1.00 0.47 0.63 0.73
## Cd 0.23 0.19 0.25 0.47 1.00 0.69 0.65
## Pb 0.13 0.07 0.21 0.63 0.69 1.00 0.77
## Zn 0.12 0.16 0.35 0.73 0.65 0.77 1.00
## Sample Size 
##    pH Al Ca Fe Cd Pb Zn
## pH 94 87 87 87 75 87 87
## Al 87 88 88 88 76 88 88
## Ca 87 88 88 88 76 88 88
## Fe 87 88 88 88 76 88 88
## Cd 75 76 76 76 76 76 76
## Pb 87 88 88 88 76 88 88
## Zn 87 88 88 88 76 88 88
## Probability values (Entries above the diagonal are adjusted for multiple tests.) 
##      pH   Al   Ca   Fe   Cd   Pb   Zn
## pH 0.00 0.03 0.00 0.06 0.32 0.72 0.72
## Al 0.00 0.00 0.03 0.00 0.51 0.72 0.51
## Ca 0.00 0.00 0.00 0.00 0.25 0.32 0.01
## Fe 0.01 0.00 0.00 0.00 0.00 0.00 0.00
## Cd 0.05 0.10 0.03 0.00 0.00 0.00 0.00
## Pb 0.24 0.50 0.05 0.00 0.00 0.00 0.00
## Zn 0.26 0.13 0.00 0.00 0.00 0.00 0.00
## 
##  To see confidence intervals of the correlations, print with the short=FALSE option

The output from psych::corTest()has three sub-tables:

  1. the correlation coefficients for each pair of variables (note symmetry)
  2. the number of pairs of observations for each relationship (some observations may be missing)
  3. the p values for each relationship (raw p-values are reported below the diagonal and p-values adjusted for multiple comparisons above the diagonal (by default based on Holm's correction.)

[Note that for Pearson correlations we instead use method="pearson" in the corTest function.]

It can be a little tricky to compare raw and adjusted p-values, so we can tidy it up with a bit of code:

corr_pvals <- corr_table$p
corr_pvals[which(corr_pvals==0)] <- NA
cat("----- Adjusted (upper) and raw (lower) p-values for correlations -----\n")
print(round(corr_pvals, 3), na.print = "")
## ----- Adjusted (upper) and raw (lower) p-values for correlations -----
##       pH    Al    Ca    Fe    Cd    Pb    Zn
## pH       0.033 0.000 0.061 0.316 0.716 0.716
## Al 0.003       0.030 0.000 0.514 0.716 0.514
## Ca 0.000 0.003       0.001 0.250 0.316 0.010
## Fe 0.007 0.000 0.000       0.000 0.000 0.000
## Cd 0.052 0.103 0.031 0.000       0.000 0.000
## Pb 0.239 0.500 0.045 0.000 0.000       0.000
## Zn 0.262 0.128 0.001 0.000 0.000 0.000

As above,the p-values give the probability of the observed relationship if the null hypothesis (i.e. no relationship) is true. Corrections are to reduce the risk of Type 1 Errors (false positives) which is greater when multiple comparisons are being made. We should always use the adjusted p-values to interpret a correlation matrix.

 

Since a correlation coefficient is a standardised measure of association, we can treat it as an 'effect size'.
Cohen (1988) suggested the following categories:

Range in r Effect size term
0 < |r| ≤ 0.1 negligible
0.1 < |r| ≤ 0.3 small
0.3 < |r| ≤ 0.5 medium
0.5 < |r| ≤ 1 large

|r| means the absolute value of r (i.e. ignoring whether r is positive or negative)

 

Correlation heatmaps

These are a handy visual way of displaying a correlation matrix. We use the corrplot() function from the R package corrplot. We'll use some different data to show a plot with both positive and negative correlations, and display the text correlation matrix after the heatmap (Figure 2) for reference.

afs23 <- read.csv(paste0(git,"afs23.csv"), stringsAsFactors = TRUE)
library(corrplot)
cormat1 <- corTest(afs23[,c("pH","EC","Al","Ca","Fe","Cu","Gd","Pb","Zn")], 
                        method="spearman")
print(cormat1$r, digits=2)
corrplot(cormat1$r, 
         method="ellipse", diag=FALSE, addCoef.col = "black", 
         tl.col = 1, tl.cex = 1.2, number.font = 1, cl.cex=1)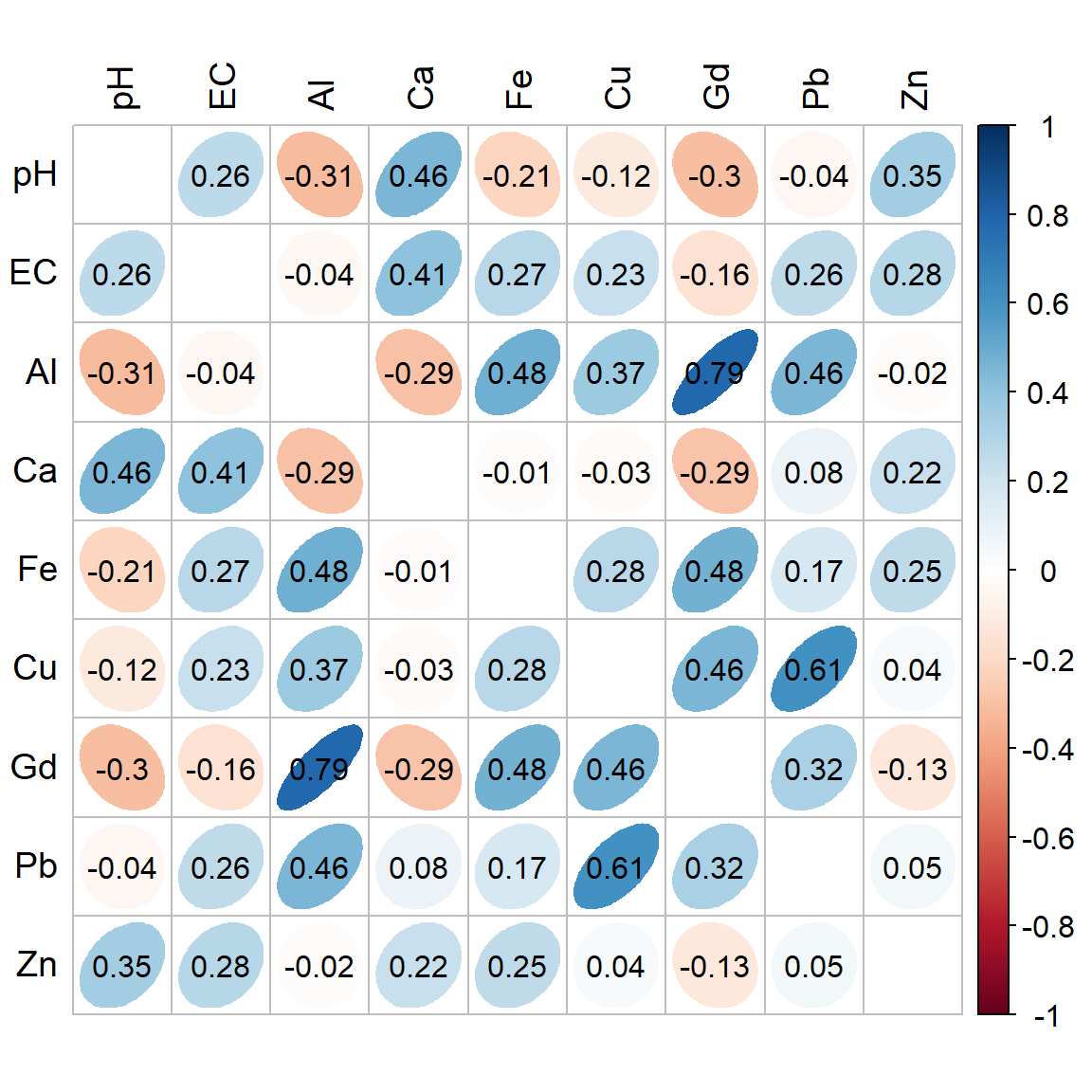
Figure 2: Correlation heatmap (Spearman) for selected variables in the 2023 Ashfield Flats sediment data. The numeric correlation matrix is below.

Figure 2: Correlation heatmap (Spearman) for selected variables in the 2023 Ashfield Flats sediment data. The numeric correlation matrix is below. 

##        pH     EC     Al     Ca     Fe     Cu    Gd     Pb     Zn
## pH  1.000  0.265 -0.311  0.456 -0.214 -0.117 -0.30 -0.043  0.350
## EC  0.265  1.000 -0.039  0.405  0.272  0.228 -0.16  0.258  0.281
## Al -0.311 -0.039  1.000 -0.292  0.481  0.369  0.79  0.457 -0.015
## Ca  0.456  0.405 -0.292  1.000 -0.014 -0.028 -0.29  0.080  0.220
## Fe -0.214  0.272  0.481 -0.014  1.000  0.278  0.48  0.173  0.253
## Cu -0.117  0.228  0.369 -0.028  0.278  1.000  0.46  0.606  0.039
## Gd -0.302 -0.158  0.786 -0.288  0.478  0.459  1.00  0.321 -0.126
## Pb -0.043  0.258  0.457  0.080  0.173  0.606  0.32  1.000  0.051
## Zn  0.350  0.281 -0.015  0.220  0.253  0.039 -0.13  0.051  1.000

 

[There is also a simpler correlation heatmap function in the psych package, cor.plot().]

We can also (with a bit of manipulation of the correlation matrix using the reshape2 package) make a heatmap in ggplot2 using geom_tile(), as shown below in Figure 3. We use the correlation matrix cormat1 generated above.

library(reshape2)
cormelt <- melt(cormat1$r) # convert mtrix to long format
cormelt$value[which(cormelt$value>=0.999999)] <- NA # remove diagonal values=1
# draw the ggplot heatmap
library(ggplot2)
ggplot(data=cormelt, aes(x=Var1, y=Var2, fill=value)) +
  geom_tile(na.rm=T, color="white", linewidth=1) + labs(x="", y="") +
  geom_text(aes(label = round(value,2)), size = 4) + 
  scale_fill_gradient2(high="steelblue", mid="white", low="firebrick", 
                       na.value="white", name="r scale") +
  theme_minimal() + theme(aspect.ratio = 1)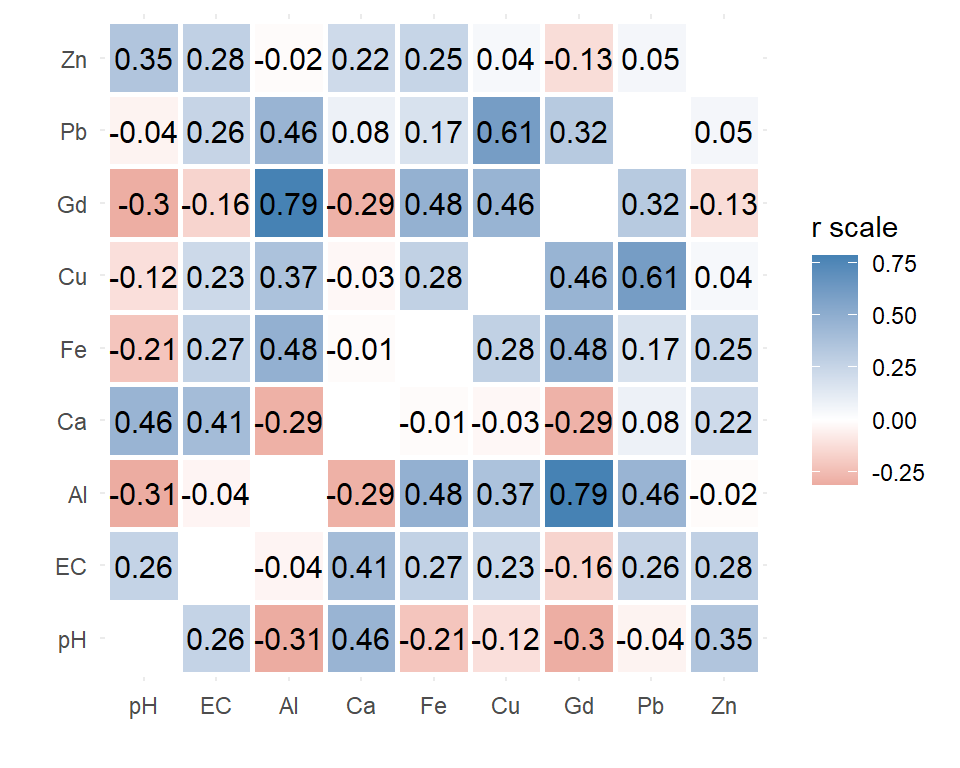
Figure 3: Correlation heatmap (Spearman) drawn using `ggplot2` for selected variables in the 2023 Ashfield Flats sediment data.

Figure 3: Correlation heatmap (Spearman) drawn using ggplot2 for selected variables in the 2023 Ashfield Flats sediment data.

 

Scatter plot matrix to check correlation matrix

It's always a good idea to plot scatterplots for the relationships we are exploring. Scatter (x-y) plots can show if:

  • a correlation coefficient is unrealistically high due to a small number of outliers, or because there are aligned (or only 2) groups of points
  • a correlation coefficient is low, not because of a lack of relationship, but because relationships differ for different groups of points;
  • there is a consistent relationship for all groups of observations.
require(car) # needed for scatterplotMatrix() function
palette(c("black",viridis::plasma(8)[2:7],"white")); carPalette(palette())
scatterplotMatrix(~pH+ log10(Al)+ log10(Ca)+ log10(Cd)+ 
                    log10(Fe)+ log10(Pb)+ log10(Zn) | Type, 
                  smooth=FALSE, ellipse=FALSE, by.groups=TRUE, 
                  col=c(4,2,1), pch=c(16,1,15), cex.lab=1.5, data=sv2017,
                  legend=list(coords="bottomleft"))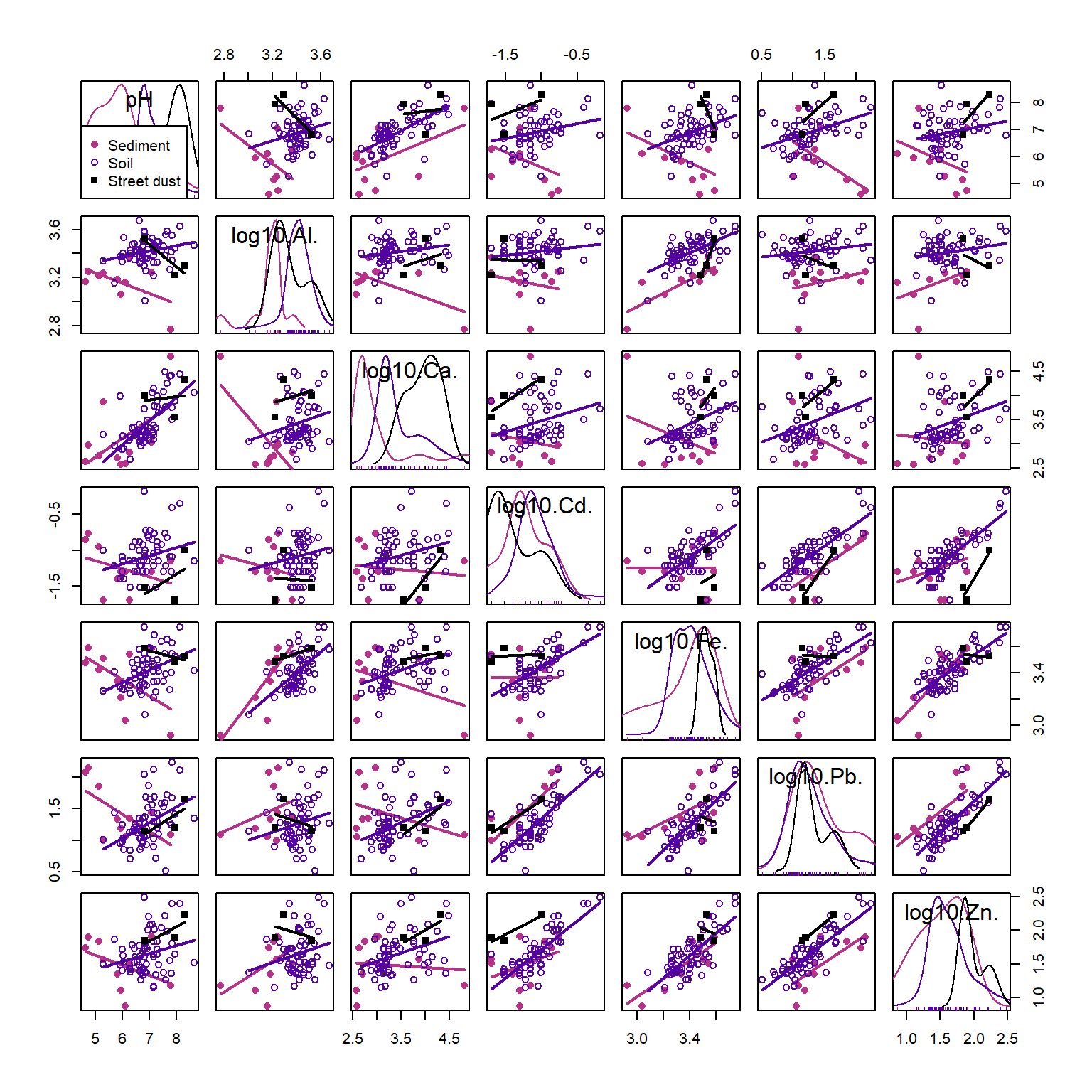
Figure 4: Scatter plot matrix for selected variables in the 2017 Smiths-Veryard sediment data, with observations and regression lines grouped by sample Type. Scatter plot matrices are a powerful exploratory data analysis tool.

Figure 4: Scatter plot matrix for selected variables in the 2017 Smiths-Veryard sediment data, with observations and regression lines grouped by sample Type. Scatter plot matrices are a powerful exploratory data analysis tool.

(See Figures 18 and 19 in the ggplot page if you want to make scatter plot matrices in ggplot2.)

 

In Figure 4, Pb and Zn are positively related (Pearson's r = 0.77, p<0.0001) independent of which group (Sediment, Soil, or Street dust) observations are from. Conversely, the relationship between pH and Cd is weak (r=0.23, adjusted p=0.32), but there appear to be closer relationships between observations from individual groups. Finally, the relationship between Al and Ca may be influenced by a single observation with low Al and high Ca. All issues like this should be considered when we explore our data more deeply.

The classic example of correlations which need plots to interpret them is the somewhat famous Anscombe's Quartet. This is shown below in Figure 5:

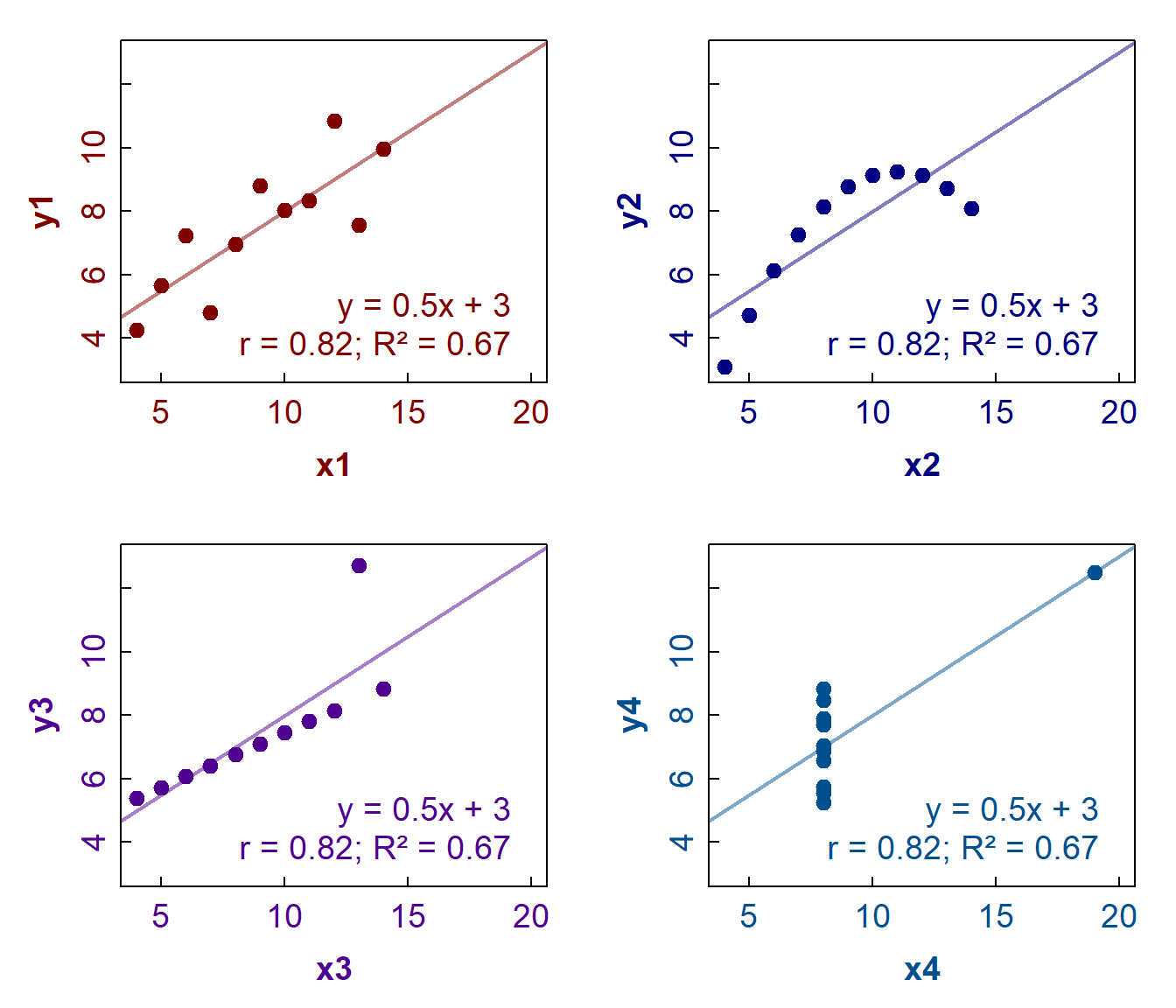
Figure 5: Anscombe's Quartet – plots of 4 distinct x-y data sets with regression lines, all having the same slope, intercept, Pearson's r, and R² values. The data are available in R via `datasets::anscombe`.

Figure 5: Anscombe's Quartet – plots of 4 distinct x-y data sets with regression lines, all having the same slope, intercept, Pearson's r, and R² values. The data are available in R via datasets::anscombe.

 

References

Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences, Second Edition. Erlbaum Associates, Hillsdale, NJ, USA.

Reimann, C., Filzmoser, P., Garrett, R.G., Dutter, R., (2008). Statistical Data Analysis Explained: Applied Environmental Statistics with R. John Wiley & Sons, Chichester, England (see Chapter 16).

 

CC-BY-SA • All content by Ratey-AtUWA. My employer does not necessarily know about or endorse the content of this website.
Created with rmarkdown in RStudio. Currently using the free yeti theme from Bootswatch.