UWA logoMaterial to support teaching in Environmental Science at The University of Western Australia

Units ENVT3361, ENVT4461, and ENVT5503

Relationships pages: Correlations | Simple linear regression | Grouped linear regression | Multiple linear regression

 

Suggested activities

Using the R code file provided and the afs1923 dataset:

💾 The afs1923 dataset in csv (comma-separated) format

🔣 R code file for this and related workshop sessions

 

Introduction

In a previous session on simple regression, we finished by suggesting that one way we could make regression prediction more accurate was by

allowing regression relationships to differ for different groups in our data (defined by a factor variable) – regression by groups

This session will continue or efforts to predict Cr from Al, but we know the data were derived from analysis of samples from diverse types of environment. For that reason, it seems reasonable to evaluate a regression model which allows the regression coefficients (intercept and slope) to differ for different sample types.

As previously, our first step is to read the data, and change anything we need to:

git <- "https://github.com/Ratey-AtUWA/Learn-R-web/raw/main/"
afs1923 <- read.csv(paste0(git,"afs1923.csv"), stringsAsFactors = TRUE)
# re-order the factor levels
afs1923$Type <- factor(afs1923$Type, levels=c("Drain_Sed","Lake_Sed","Saltmarsh","Other"))
afs1923$Type2 <- 
  factor(afs1923$Type2, 
         levels=c("Drain_Sed","Lake_Sed","Saltmarsh W","Saltmarsh E","Other"))

Next, we inspect a scatterplot of the variables which matches the kind of regression model we intend to apply (Figure 1):

library(car)
par(mar=c(3,3,0.5,0.5), mgp=c(1.3,0.2,0), tcl=0.2, font.lab=2)
scatterplot(Cr ~ Al | Type2, data=afs1923, smooth=FALSE,
            col=inferno(nlevels(afs1923$Type2), end=0.75), pch=c(5,17,15,19,10), 
            legend=list(coords="bottomright", title="Sample type"))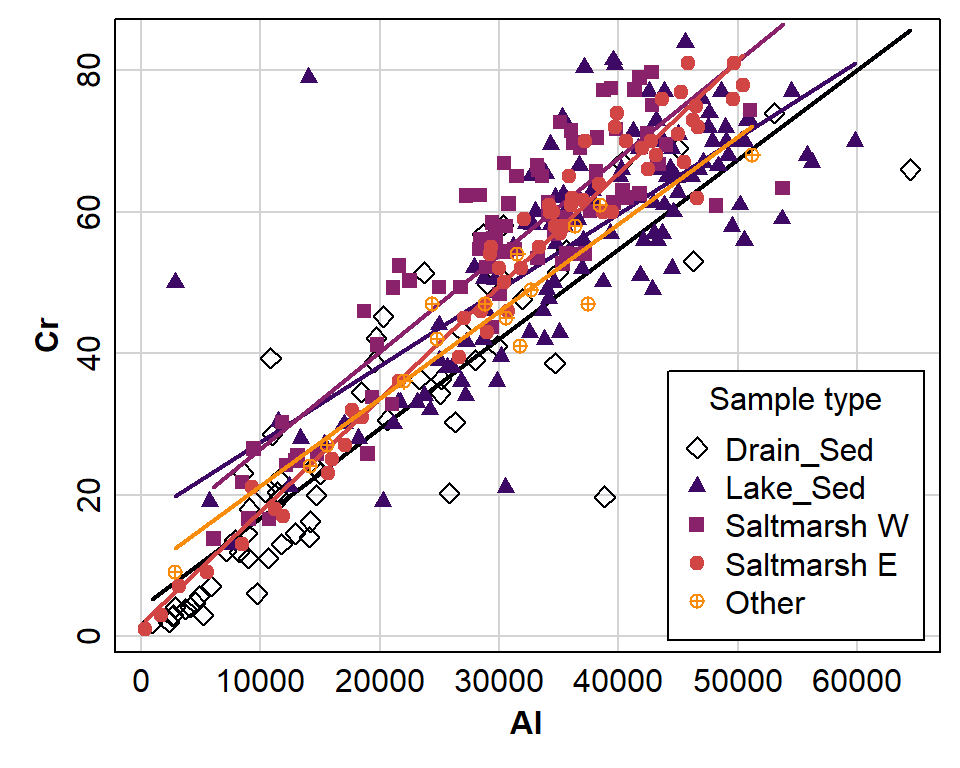
Figure 1: Different relationships predicting Cr from Al depending on the sample type (data from analysis of sediments from Ashfield Flats, 2019-2023.

Figure 1: Different relationships predicting Cr from Al depending on the sample type (data from analysis of sediments from Ashfield Flats, 2019-2023.

Predicting chromium from aluminium using a regression model which varies by groups

Note the syntax used to separate by factor categories:

lmCrAl_byType <- lm(Cr ~ Al * Type2, data=afs1923)
summary(lmCrAl_byType)
## 
## Call:
## lm(formula = Cr ~ Al * Type2, data = afs1923)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -33.644  -5.039  -0.195   4.637  47.183 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          4.069e+00  1.845e+00   2.205  0.02813 *  
## Al                   1.268e-03  7.872e-05  16.114  < 2e-16 ***
## Type2Lake_Sed        1.264e+01  3.166e+00   3.994 8.04e-05 ***
## Type2Saltmarsh W     8.628e+00  3.507e+00   2.460  0.01440 *  
## Type2Saltmarsh E    -2.367e+00  3.366e+00  -0.703  0.48231    
## Type2Other           4.806e+00  6.162e+00   0.780  0.43600    
## Al:Type2Lake_Sed    -1.928e-04  1.036e-04  -1.861  0.06362 .  
## Al:Type2Saltmarsh W  1.056e-04  1.209e-04   0.873  0.38318    
## Al:Type2Saltmarsh E  3.282e-04  1.140e-04   2.880  0.00424 ** 
## Al:Type2Other       -3.437e-05  2.091e-04  -0.164  0.86954    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.444 on 325 degrees of freedom
## Multiple R-squared:  0.8362, Adjusted R-squared:  0.8317 
## F-statistic: 184.4 on 9 and 325 DF,  p-value: < 2.2e-16

This is similar output to simple linear regression in the previous example, but the Coefficients: table is much more complicated.

Compare the two models

Sometimes models can have greater R2 but only because we've made them more complex by grouping our observations or by adding more predictors. We want the simplest model possible. We compare the models using an analysis of variance with the anova() function (where the null hypothesis is equal predictive ability). The models compared need to be nested, that is, one is a subset of the other.

Before we do this, we need to re-create the simple model from a previous session:

lmCrAlsimple <- lm(Cr ~ Al, data=afs1923)
summary(lmCrAlsimple)
## 
## Call:
## lm(formula = Cr ~ Al, data = afs1923)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -40.751  -5.349  -0.251   5.774  52.250 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.672e+00  1.284e+00   5.976 5.89e-09 ***
## Al          1.359e-03  3.829e-05  35.480  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.428 on 333 degrees of freedom
## Multiple R-squared:  0.7908, Adjusted R-squared:  0.7902 
## F-statistic:  1259 on 1 and 333 DF,  p-value: < 2.2e-16

So our more complex (grouped) linear model has greater R2 (0.836) than the simple linear model (R2 = 0.791). We now perform the anova test to see whether this improvement is significant:

anova(lmCrAlsimple, lmCrAl_byType)
## Analysis of Variance Table
## 
## Model 1: Cr ~ Al
## Model 2: Cr ~ Al * Type2
##   Res.Df   RSS Df Sum of Sq      F    Pr(>F)    
## 1    333 29599                                  
## 2    325 23174  8    6424.7 11.263 4.366e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The p-value (Pr(>F)) is ≃ 4.4×10−14, i.e. below 0.05, so we reject H0 that the models have equivalent predictive ability. In that case the model which explains more variance in the dependent variable Cr is best; that is, the grouped linear model with R2 = 0.836 (i.e., explaining 83.6% of the variance in Cr based on the variance in Al divided into groups by the factor Type2).

The choice of models should be based on an interpretation of “Occam's Razor” a.k.a. the “Principle of Parsimony”:

“Plurality must never be posited without necessity.”
— William of Ockham (also spelled Occam) (1285 - 1348), English theologian, logician, and Franciscan friar

In practice this means that if more than one hypothesis or model explains our data equally well, we should always choose the simplest one.

Another way we can test for the most appropriate model is by using the AIC or Aikake Information Criterion, which ‘penalises’ a model having more parameters. A better model will have a lower value of AIC, and the built-in penalty means that for equivalent models (i.e. non-significant ANOVA) the model with more parameters will have greater AIC, and so we should select the simpler model with the least AIC value. For our two models, AIC shoud still be lower for the more complex model (otherwise we are in trouble, since the ANOVA and AIC would disagree, and then which one would we choose?). Anyway, let's find out:

AIC(lmCrAlsimple, lmCrAl_byType)
##               df      AIC
## lmCrAlsimple   3 2457.942
## lmCrAl_byType 11 2391.968

The output from the AIC() function shows that even though the degrees of freedom df for the grouped model (11) is much greater than for the simple model (3), the grouped model still has a lower AIC value (≃2392) than the simple model (≃2456). So, the ANOVA and AIC do agree after all 😌.

We can see a little more detail about the individual group-wise relationships or ‘effects’ by plotting an effects plot using functions from the effects package (Figure 2):

library(effects)
plot(allEffects(lmCrAl_byType))
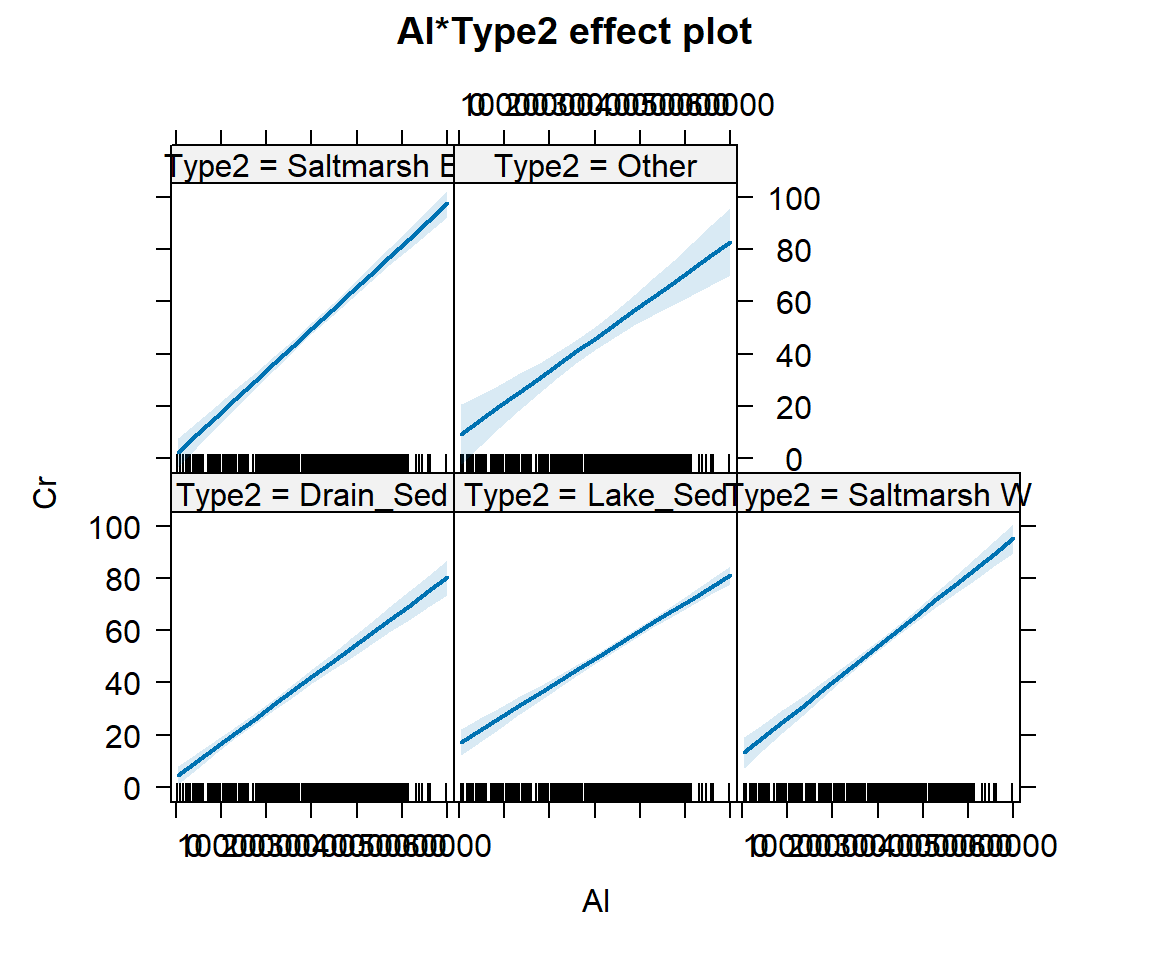
Figure 2: Effect plots showing the effects of interacting predictors `Al * Type2` on Cr, using data from sediments at Ashfield Flats 2019-2023.

Figure 2: Effect plots showing the effects of interacting predictors Al * Type2 on Cr, using data from sediments at Ashfield Flats 2019-2023.

So even though the plots in Figure 1 and Figure 2 suggest that each group has a similar Cr ~ Al relationship, the slopes and intercepts differ enough between groups to give an improved prediction over the simple model.

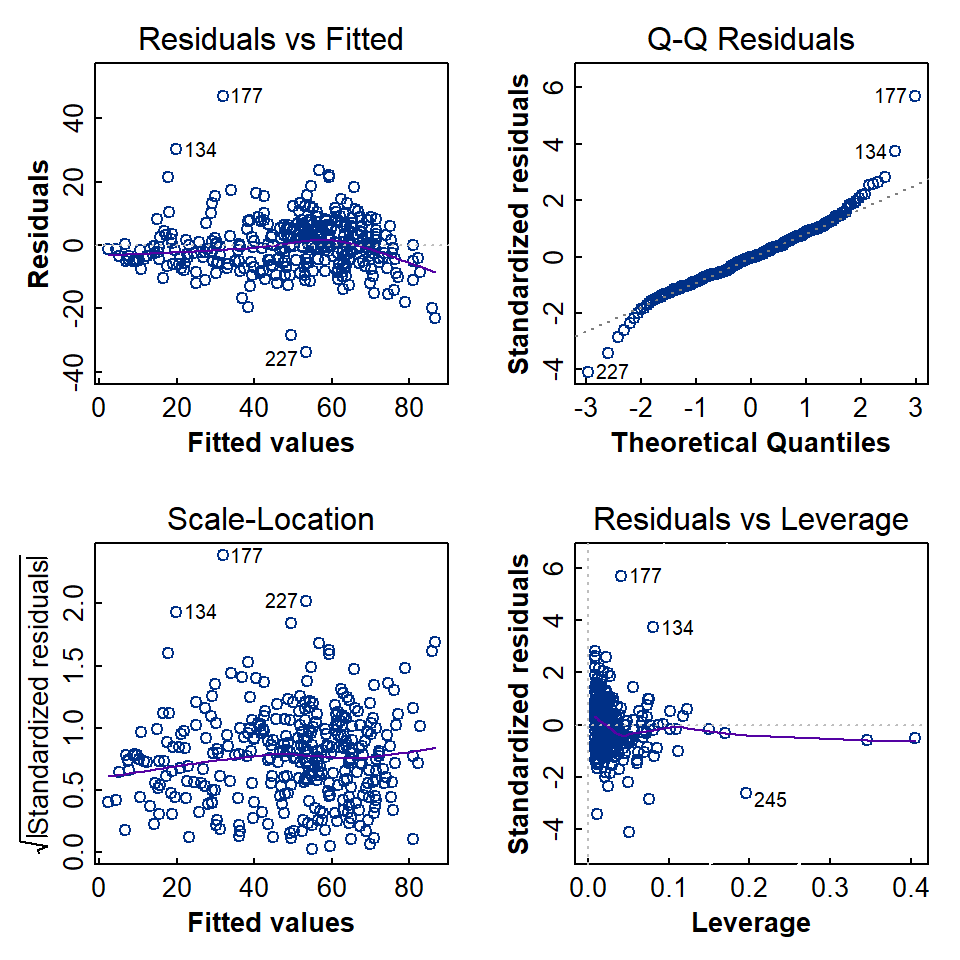
Regression assumptions

The assumptions implicit in linear regression were presented in the session on simple linear regression models. We run the same set of diagnostic tests on more complex regression models as well.

Diagnostic plots for Grouped linear regression, Cr ~ Al * Type2

par(mfrow=c(2,2), mar=c(3,3,2,1), mgp=c(1.3,0.2,0), tcl=0.2, font.lab=2)
plot(lmCrAl_byType, col="#003087")
Diagnostic plots for a grouped linear model predicting Cr from Al with obervations grouped by sample type.

Diagnostic plots for a grouped linear model predicting Cr from Al with obervations grouped by sample type.

Formal statistical tests of regression assumptions

As with simple linear regression, we can test all of the assumptions with formal statistical tests (see the simple linear regression session for explanations and null hypotheses).

shapiro.test(lmCrAl_byType$residuals) # normality
## 
##  Shapiro-Wilk normality test
## 
## data:  lmCrAl_byType$residuals
## W = 0.95798, p-value = 3.26e-08
require(lmtest)
bgtest(lmCrAl_byType) # autocorrelation (independence)
## 
##  Breusch-Godfrey test for serial correlation of order up to 1
## 
## data:  lmCrAl_byType
## LM test = 52.363, df = 1, p-value = 4.613e-13
bptest(lmCrAl_byType) # homoscedasticity
## 
##  studentized Breusch-Pagan test
## 
## data:  lmCrAl_byType
## BP = 36.366, df = 9, p-value = 3.413e-05
raintest(lmCrAl_byType) # linearity
## 
##  Rainbow test
## 
## data:  lmCrAl_byType
## Rain = 0.51147, df1 = 168, df2 = 157, p-value = 1
require(car)
outlierTest(lmCrAl_byType) # influential observations (outliers)
##      rstudent unadjusted p-value Bonferroni p
## 177  6.003042         5.1884e-09   1.7381e-06
## 227 -4.192086         3.5701e-05   1.1960e-02
summary(cooks.distance(lmCrAl_byType)) # influential observations
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 0.0000000 0.0001556 0.0007584 0.0036023 0.0022228 0.1662896
infl.lmCrAl <- influence.measures(lmCrAl_byType)
ninf <- nrow(summary(infl.lmCrAl)) # number of possibly influential observations
modform <- deparse(lmCrAl_byType$call)
rninf <- row.names(summary(infl.lmCrAl)) # IDs of possibly influential observations
# if you run this code chunk yourself you will see the whole summary(infl.lmCrAl) output
cat(paste0("For the model '", modform, "' there are ", ninf, 
           " potentially influential observations.\n\n"))
cat("The", ninf, "rows containing potentially influential obervations are:\n"); as.integer(rninf)
## For the model 'lm(formula = Cr ~ Al * Type2, data = afs1923)' there are 36 potentially influential observations.
## 
## The 36 rows containing potentially influential obervations are:
##  [1]   2  56  92 134 137 138 139 168 177 190 196 218 219 220 227 236 245 250 251 252 273 290 291
## [24] 296 297 298 316 317 318 319 320 321 322 323 324 325

To summarise:

Table 1: Summary of regression diagnostic tests for a grouped linear model predicting Cr from Al (grouped by Type) in sediments from Ashfield Flats Reserve, based on data from samples collected from 2019-2023.

Test

Assessing

Results

Shapiro-Wilk

Are residuals normally distributed?

No (qq-plot suggests long tails)

Breusch-Godfrey

Are residuals independent?

No, there is autocorrelation

Breusch-Pagan

Are residuals homoscedastic?

No (p<0.05)

Rainbow

Is the relationship linear?

Yes (p>0.05)

Outlier

Are there significant outliers (Bonferroni)?

2 points are possible outliers

Cook's Distance

Are there any potentially influential observations?

No (no values > 0.5)

Infuence Measures

Are there any potentially influential observations?

Yes (36 out of 335 observations)

 

The summary of the diagnostic tests in Table 1 shows that not all the formal assumptions of regression are fulfilled by our model. Even though the model may not be strictly statistically valid, the regression output showed that ≃ 84% of the variance in Cr could be explained by Al when observations were grouped by sample type. So, from a practical perspective, this grouped regression model could also be used for prediction, and the greater R2 makes it a better prediction option than the simple model discussed in another session.

The next option would be a model which has more than one predictor variable for our dependent variable – multiple regression.

 

References

Fox, J. and Weisberg, S. (2019). An {R} Companion to Applied Regression, Third Edition. Thousand Oaks CA: Sage. https://socialsciences.mcmaster.ca/jfox/Books/Companion/ (R package car)

Garnier S, Ross N, Rudis R, Camargo AP, Sciaini M, Scherer C (2021). Rvision – Colorblind-Friendly Color Maps for R. R package version 0.6.2. (R package viridis)

Reimann, C., Filzmoser, P., Garrett, R.G., Dutter, R., (2008). Statistical Data Analysis Explained: Applied Environmental Statistics with R. John Wiley & Sons, Chichester, England (see Chapter 16).

Zeileis, A. and Hothorn, T. (2002). Diagnostic Checking in Regression Relationships. R News 2(3), 7-10. https://CRAN.R-project.org/doc/Rnews/ (R package lmtest)

 

CC-BY-SA • All content by Ratey-AtUWA. My employer does not necessarily know about or endorse the content of this website.
Created with rmarkdown in RStudio. Currently using the free yeti theme from Bootswatch.