See also my other GitHub Pages website dedicated to teaching: “R for Environmental Science”.

Correlation & regression 1

Basic correlation analyses

Let's look at the relationship between Cd and Zn in the Smiths Lake and Charles Veryard Reserves data from 2017.
For Pearson's correlation we need variables with normal distributions, so first log₁₀-transform Cd and Zn...

sv2017 <- read.csv("sv2017_original.csv", stringsAsFactors = TRUE)
sv2017$Cd.log <- log10(sv2017$Cd)
sv2017$Zn.log <- log10(sv2017$Zn)

...and test if the distributions are normal. Remember that the null hypothesis for the Shapiro-Wilk test is that "the distribution of the variable of interest is not different from a normal distribution". So, if the P-value ≥ 0.05, we can't reject the null and therefore our variable is normally distributed.

shapiro.test(sv2017$Cd)
shapiro.test(sv2017$Cd.log)
shapiro.test(sv2017$Zn)
shapiro.test(sv2017$Zn.log)

##
##  Shapiro-Wilk normality test
##
## data:  sv2017$Cd
## W = 0.63001, p-value = 1.528e-12
##
##
##  Shapiro-Wilk normality test
##
## data:  sv2017$Cd.log
## W = 0.97272, p-value = 0.1006
##
##
##  Shapiro-Wilk normality test
##
## data:  sv2017$Zn
## W = 0.6155, p-value = 7.75e-14
##
##
##  Shapiro-Wilk normality test
##
## data:  sv2017$Zn.log
## W = 0.9828, p-value = 0.295

Pearson's r changes with transformation

cor.test(sv2017$Cd, sv2017$Zn, alternative="two.sided",
         method="pearson") # is Pearson valid?
cor.test(sv2017$Cd.log, sv2017$Zn.log, alternative="two.sided",
         method="pearson") # is Pearson valid?

##
##  Pearson's product-moment correlation
##
## data:  sv2017$Cd and sv2017$Zn
## t = 9.8415, df = 74, p-value = 4.357e-15
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.6353031 0.8363947
## sample estimates:
##       cor
## 0.7529165
##
##
##  Pearson's product-moment correlation
##
## data:  sv2017$Cd.log and sv2017$Zn.log
## t = 7.696, df = 74, p-value = 4.859e-11
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.5193717 0.7756160
## sample estimates:
##       cor
## 0.6667536

For the Pearson correlation we get a t statistic and associated degrees of freedom (df), for which there is a p-value. The null hypothesis is that there is "no relationship between the two variables", which we can reject if p ≤ 0.05. We also get a 95% confidence interval for the correlation coefficient, and finally an estimate of Pearson's r (cor).

A Spearman coefficient doesn't change with transformation, since it is calculated from the ranks (ordering) of each variable.

cor.test(sv2017$Cd, sv2017$Zn, alternative="two.sided",
         method="spearman") # can we use method="pearson"?
cor.test(sv2017$Cd.log, sv2017$Zn.log, alternative="two.sided",
         method="spearman") # can we use method="pearson"?

##
##  Spearman's rank correlation rho
##
## data:  sv2017$Cd and sv2017$Zn
## S = 25750, p-value = 2.494e-10
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho
## 0.6479832
##
##
##  Spearman's rank correlation rho
##
## data:  sv2017$Cd.log and sv2017$Zn.log
## S = 25750, p-value = 2.494e-10
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho
## 0.6479832

For the Spearman correlation we get an S statistic and associated p-value. The null hypothesis is that there is no relationship between the two variables, which we can reject if p ≤ 0.05. We also get an estimate of Spearman's rho (analogous to Pearson's r).

Simple scatterplot by groups

We're using base R to plot - you might like to try using scatterplot() from the car package.

Before plotting, we first set our desired colour palette (optional) and graphics parameters (optional, but useful and recommended!). We end up with the plot in Figure 1:

palette(c("black","blue","red3","darkgreen","purple",
          "darkcyan","sienna3","grey50","white"))
par(mfrow=c(1,1), mar=c(3,3,1,1), mgp=c(1.5,0.3,0), oma=c(0,0,0,0), tcl=0.2,
    cex=1.2, cex.lab=1.2, cex.axis=1., lend="square", ljoin="mitre", font.lab=2)

# . . . then plot the data
plot(sv2017$Cd~sv2017$Zn, col=c(6,7,1)[sv2017$Type], log="xy",
     pch=c(16,1,15)[sv2017$Type], lwd=c(1,2,1)[sv2017$Type], cex=1.25,
     xlab="Zn (mg/kg)", ylab="Cd (mg/kg)")
abline(lm(sv2017$Cd.log~sv2017$Zn.log)) # line of best fit
legend("topleft", legend=c(levels(sv2017$Type),"Best-fit line ignoring Type"),
       cex=1, col=c(6,7,1,1),
       pch=c(16,1,15,NA), pt.lwd=c(1,2,1), lwd = c(NA,NA,NA,1),
       pt.cex=1.25, bty="n", inset=0.02,
       title=expression(italic("Sample Type")))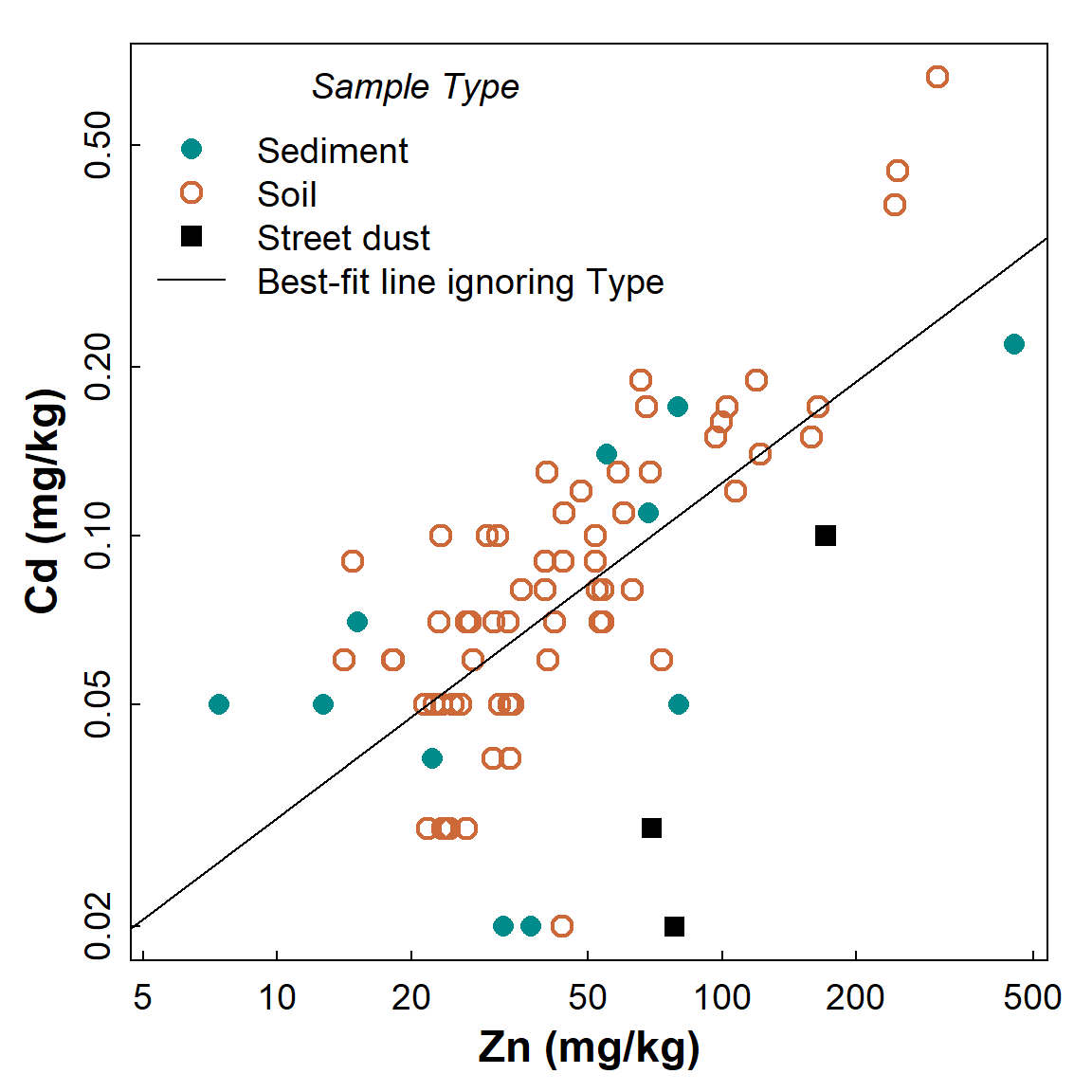

Figure 1: Scatterplot showing the relationship between Cd and Zn, with observations identified by Type but showing the regression line for all data independent of grouping.

"The invalid assumption that correlation implies cause is probably among the two or three most serious and common errors of human reasoning."

--- Stephen Jay Gould

Correlation matrix - two ways of doing it

We'll generate Spearman correlation matrices in these examples, but it's easy to change the code to generate Pearson (or other) correlation matrices.
The p-values give the probability of the observed relationship if the null hypothesis (i.e. no relationship) is true.

require(Hmisc) # needed for rcorr() function
corr_table <- rcorr(as.matrix(sv2017[c("pH","Al","Ca","Fe","Cd","Pb","Zn")]),
                    type="spearman")
print(corr_table)

##      pH   Al   Ca   Fe   Cd   Pb   Zn
## pH 1.00 0.31 0.68 0.29 0.23 0.13 0.12
## Al 0.31 1.00 0.32 0.45 0.19 0.07 0.16
## Ca 0.68 0.32 1.00 0.42 0.25 0.21 0.35
## Fe 0.29 0.45 0.42 1.00 0.47 0.63 0.73
## Cd 0.23 0.19 0.25 0.47 1.00 0.69 0.65
## Pb 0.13 0.07 0.21 0.63 0.69 1.00 0.77
## Zn 0.12 0.16 0.35 0.73 0.65 0.77 1.00
##
## n
##    pH Al Ca Fe Cd Pb Zn
## pH 94 87 87 87 75 87 87
## Al 87 88 88 88 76 88 88
## Ca 87 88 88 88 76 88 88
## Fe 87 88 88 88 76 88 88
## Cd 75 76 76 76 76 76 76
## Pb 87 88 88 88 76 88 88
## Zn 87 88 88 88 76 88 88
##
## P
##    pH     Al     Ca     Fe     Cd     Pb     Zn
## pH        0.0033 0.0000 0.0068 0.0517 0.2385 0.2622
## Al 0.0033        0.0028 0.0000 0.1028 0.5000 0.1282
## Ca 0.0000 0.0028        0.0000 0.0312 0.0451 0.0008
## Fe 0.0068 0.0000 0.0000        0.0000 0.0000 0.0000
## Cd 0.0517 0.1028 0.0312 0.0000        0.0000 0.0000
## Pb 0.2385 0.5000 0.0451 0.0000 0.0000        0.0000
## Zn 0.2622 0.1282 0.0008 0.0000 0.0000 0.0000

The output has three sub-tables:

the correlation coefficients for each pair of variables (note symmetry)
the number of pairs of observations for each relationship (some observations may be missing)
the p values for each relationship (note symmetry)

[Note that for Pearson correlations we instead use type="pearson" in the rcorr function.]

Since a correlation coefficient is a standardised measure of association, we can treat it as an 'effect size'.
Cohen (1988) suggested the following categories:

Range in r			Effect size term
0 <	\|r\|	≤ 0.1	negligible
0.1 <	\|r\|	≤ 0.3	small
0.3 <	\|r\|	≤ 0.5	medium
0.5 <	\|r\|	≤ 1	large

|r| means the absolute value of r (i.e. ignoring whether r is positive or negative)

Correlation matrix with p-values corrected for multiple comparisons

We can do this using the rcorr.adjust() function in the RcmdrMisc package which calculates corrected P-values. As above,the p-values give the probability of the observed relationship if # the null hypothesis (i.e. no relationship) is true. Corrections are to reduce the risk of Type 1 Errors (false positives) which is greater when multiple comparisons are being made.

We include use="pairwise.complete" in the rcorr.adjust() function parameters, otherwise the correlations are calculated on the number of observations for the variable with the most missing values (try changing it after reading help("rcorr.adjust")).

require(RcmdrMisc) # needed for rcorr.adjust() function
rcorr.adjust(sv2017[c("pH","Al","Ca","Fe","Cd","Pb","Zn")], type="spearman",
             use="pairwise.complete")

##
##  Spearman correlations:
##        pH     Al     Ca     Fe     Cd     Pb     Zn
## pH 1.0000 0.3112 0.6763 0.2884 0.2256 0.1277 0.1215
## Al 0.3112 1.0000 0.3153 0.4470 0.1886 0.0728 0.1634
## Ca 0.6763 0.3153 1.0000 0.4155 0.2474 0.2142 0.3498
## Fe 0.2884 0.4470 0.4155 1.0000 0.4739 0.6267 0.7340
## Cd 0.2256 0.1886 0.2474 0.4739 1.0000 0.6935 0.6480
## Pb 0.1277 0.0728 0.2142 0.6267 0.6935 1.0000 0.7685
## Zn 0.1215 0.1634 0.3498 0.7340 0.6480 0.7685 1.0000
##
##  Number of observations:
##    pH Al Ca Fe Cd Pb Zn
## pH 94 87 87 87 75 87 87
## Al 87 88 88 88 76 88 88
## Ca 87 88 88 88 76 88 88
## Fe 87 88 88 88 76 88 88
## Cd 75 76 76 76 76 76 76
## Pb 87 88 88 88 76 88 88
## Zn 87 88 88 88 76 88 88
##
##  Pairwise two-sided p-values:
##    pH     Al     Ca     Fe     Cd     Pb     Zn
## pH        0.0033 <.0001 0.0068 0.0517 0.2385 0.2622
## Al 0.0033        0.0028 <.0001 0.1028 0.5000 0.1282
## Ca <.0001 0.0028        <.0001 0.0312 0.0451 0.0008
## Fe 0.0068 <.0001 <.0001        <.0001 <.0001 <.0001
## Cd 0.0517 0.1028 0.0312 <.0001        <.0001 <.0001
## Pb 0.2385 0.5000 0.0451 <.0001 <.0001        <.0001
## Zn 0.2622 0.1282 0.0008 <.0001 <.0001 <.0001
##
##  Adjusted p-values (Holm's method)
##    pH     Al     Ca     Fe     Cd     Pb     Zn
## pH        0.0334 <.0001 0.0608 0.3158 0.7155 0.7155
## Al 0.0334        0.0305 0.0002 0.5140 0.7155 0.5140
## Ca <.0001 0.0305        0.0007 0.2498 0.3158 0.0100
## Fe 0.0608 0.0002 0.0007        0.0002 <.0001 <.0001
## Cd 0.3158 0.5140 0.2498 0.0002        <.0001 <.0001
## Pb 0.7155 0.7155 0.3158 <.0001 <.0001        <.0001
## Zn 0.7155 0.5140 0.0100 <.0001 <.0001 <.0001

The output from rcorr.adjust() has a fourth sub-table:

the adjusted p-values for each pair of variables, which depend on the number of variables being compared

Scatter plot matrix to check correlation matrix

It's always a good idea to plot scatterplots for the relationships we are exploring. Scatter (x-y) plots can show if:

a correlation coefficient is unrealistically high due to a small number of outliers, or because there are aligned groups of points
a correlation coefficient is low, not because of a lack of relationship, but because relationships differ for different groups of points;
there is a consistent relationship for all groups of observations.

require(car) # needed for scatterplotMatrix() function
carPalette(palette())
scatterplotMatrix(~pH+ log10(Al)+ log10(Ca)+ log10(Cd)+
                    log10(Fe)+ log10(Pb)+ log10(Zn) | Type,
                  smooth=FALSE, ellipse=FALSE, by.groups=TRUE,
                  col=c(6,7,1), pch=c(16,1,15), cex.lab=1.5, data=sv2017,
                  legend=list(coords="bottomleft"))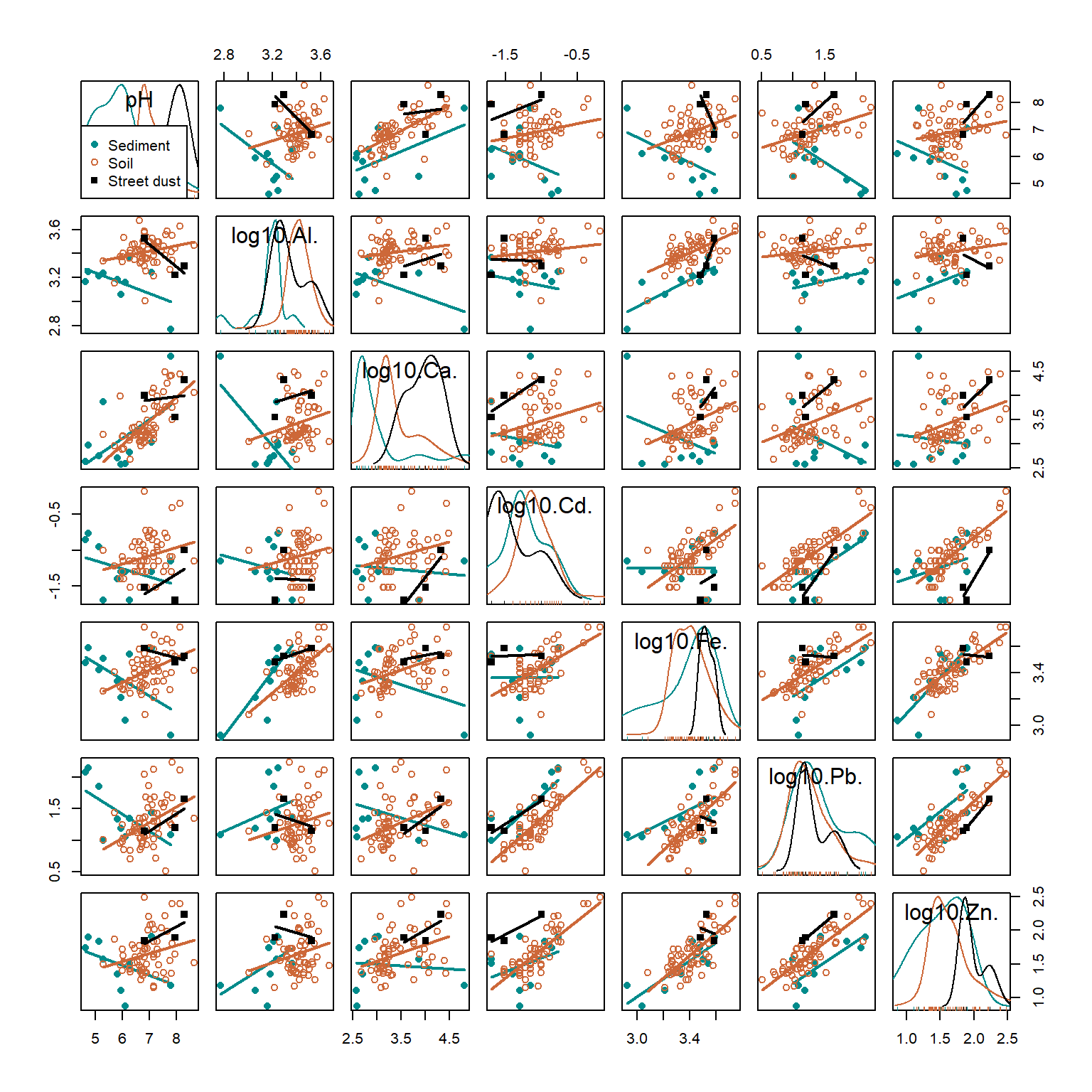

Figure 2: Scatter plot matrix for selected variables in the 2017 Smiths-Veryard sediment data, with observations and regression lines grouped by sample Type. Scatter plot matrices are a powerful exploratory data analysis tool.

In Figure 2, Pb and Zn are positively related (Pearson's r = 0.77, p<0.0001) independent of which group (Sediment, Soil, or Street dust) observations are from. Conversely, the relationship between pH and Cd is weak (r=0.23, adjusted p=0.32), but there appear to be closer relationships between observations from individual groups. Finally, the relationship between Al and Ca may be influenced by a single observation with low Al and high Ca. All issues like this should be considered when we explore our data more deeply.

Linear Regression

We will first make a simple linear regression model predicting chromium from iron.

We first create log-transformed variable columns and inspect the scatterplot (Figure 3).

par(mfrow=c(1,1), mar=c(3,3,1,1), mgp=c(1.5,0.5,0), oma=c(0,0,0,0), tcl=0.2,
    cex=1.2, cex.lab=1.2, cex.axis=1., lend="square", ljoin="mitre", font.lab=2)
carPalette(palette())
sv2017$Fe.log <- log10(sv2017$Fe)
sv2017$Cr.log <- log10(sv2017$Cr)
scatterplot(Cr ~ Fe | Type, data = sv2017,
            log = "xy", smooth = FALSE, col = c(6,7,1),
            xlab = "Fe (mg/kg)", ylab = "Cr (mg/kg)",
            legend = list(coords = "bottomright"))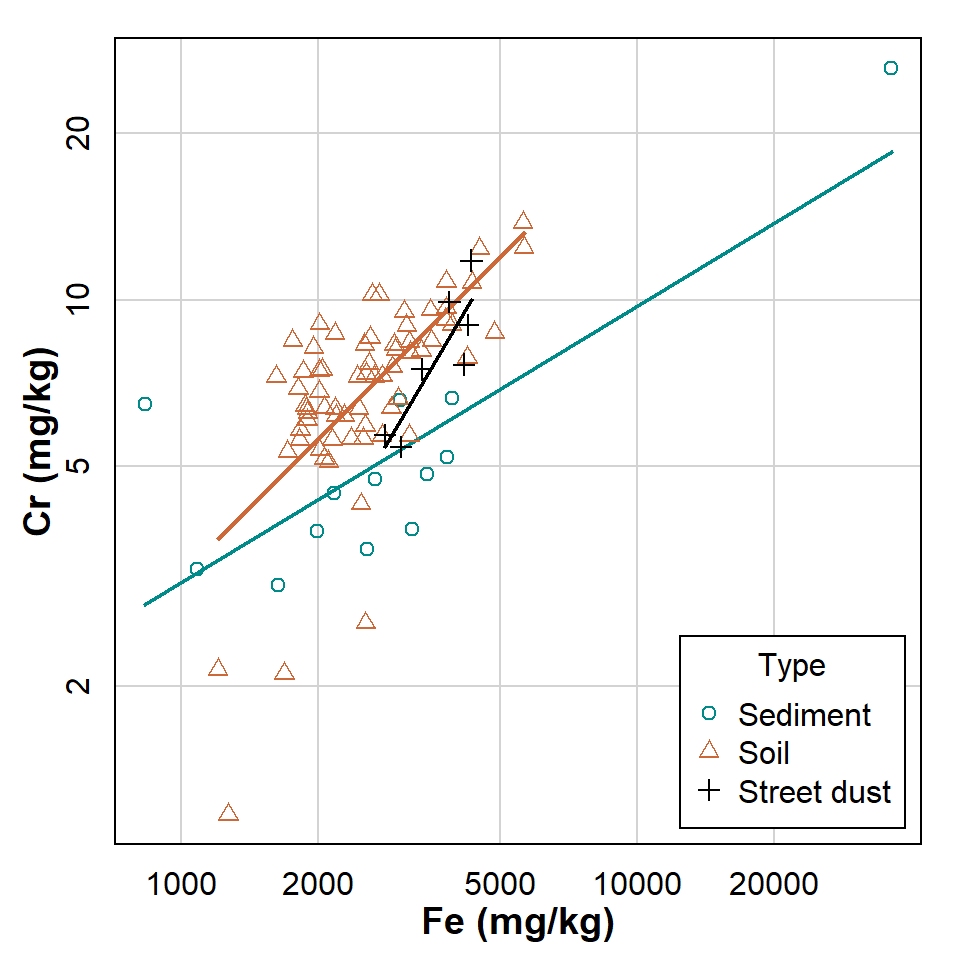

Figure 3: Scatterplot showing relationship between Cr and Fe at Smiths Lake and Charles Veryard Reserves in 2017. Observations and regression lines are separated by sample Type.

What do the ungrouped scatterplot and regression line look like?

Next use the lm() function to create a linear model object (give it a sensible name), then summarise it:

lmCrFesimple <- with(sv2017, lm(Cr.log ~ Fe.log))
summary(lmCrFesimple)

##
## Call:
## lm(formula = Cr.log ~ Fe.log)
##
## Residuals:
##      Min       1Q   Median       3Q      Max
## -0.55661 -0.05466  0.02879  0.08074  0.29981
##
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.29069    0.26753  -4.825 6.02e-06 ***
## Fe.log       0.61714    0.07795   7.917 7.78e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1428 on 86 degrees of freedom
##   (7 observations deleted due to missingness)
## Multiple R-squared:  0.4216, Adjusted R-squared:  0.4148
## F-statistic: 62.68 on 1 and 86 DF,  p-value: 7.781e-12

The output from a linear model summary in R is quite extensive:

Call: gives the model we specified (for checking)
Residuals: some summary statistics for the difference of the model from the measured values -- these differences are called the residuals
Coefficients: a table showing the parameters of the line of best fit, shown by the estimates. The intercept of the line is in the first row, and the slope labelled by the predictor variable. The other columns in the sub-table give the uncertainty in the parameters (Std.Error), and the null hypothesis p-value (Pr(>|t|)) based on a t-statistic for each parameter (against H₀ that there is no effect of a predictor, i.e. the slope = 0)
Signif. codes: just explains the asterisks *** or ** or *
The last block of text contains information on how well the model fits the data. We will focus on the R² (R-squared) value, which is equivalent to the proportion of variance in the dependent variable (Cr.log in this example) which is explained by the predictor (Fe.log in this example). We should also note the overall p-value, based on the variance ratio F-statistic, which tests H₀ = no effect of any predictor.

Predicting chromium from iron using a regression model which varies by groups

Note the syntax used to separate by factor categories:

lmCrFe_byType <- with(sv2017, lm(Cr.log ~ Fe.log * Type))
summary(lmCrFe_byType)

##
## Call:
## lm(formula = Cr.log ~ Fe.log * Type)
##
## Residuals:
##      Min       1Q   Median       3Q      Max
## -0.51934 -0.05220  0.00966  0.06412  0.36227
##
## Coefficients:
##                        Estimate Std. Error t value Pr(>|t|)
## (Intercept)            -1.01178    0.33679  -3.004  0.00353 **
## Fe.log                  0.50026    0.09695   5.160 1.69e-06 ***
## TypeSoil               -0.95452    0.51248  -1.863  0.06611 .
## TypeStreet dust        -3.05957    2.51208  -1.218  0.22674
## Fe.log:TypeSoil         0.32254    0.14910   2.163  0.03343 *
## Fe.log:TypeStreet dust  0.89402    0.70545   1.267  0.20864
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1309 on 82 degrees of freedom
##   (7 observations deleted due to missingness)
## Multiple R-squared:  0.5367, Adjusted R-squared:  0.5084
## F-statistic:    19 on 5 and 82 DF,  p-value: 1.676e-12

This is similar output to simple linear regression in the previous example, but the Coefficients: table is much more complicated.

The first two rows of the Coefficients: table under the headings give the intercept and slope for the 'base case', which by default is the first group in the factor separating the groups. In this example the first level of the factor 'Type' is 'sediment' (frustratingly, the output does not show this).
The next rows, starting with the factor name (i.e. TypeSoil and TypeStreetDust), show the difference between the intercepts for 'Soil' and 'Street dust' groups compared with the base case.
Similarly, the final rows, beginning with the predictor variable name (Fe.log:TypeSoil and Fe.log:TypeStreet dust), show the difference between the slopes for 'Soil' and 'Street dust' groups compared with the base case.

Compare the two models

Sometimes models can have greater R² but only because we've made them more complex by grouping our observations or by adding more predictors. We want the simplest model possible. We compare the models using an analysis of variance with the anova() function (where the null hypothesis is equal predictive ability). The models compared need to be nested, that is, one is a subset of the other.

anova(lmCrFesimple,lmCrFe_byType)

## Analysis of Variance Table
##
## Model 1: Cr.log ~ Fe.log
## Model 2: Cr.log ~ Fe.log * Type
##   Res.Df    RSS Df Sum of Sq      F   Pr(>F)
## 1     86 1.7539
## 2     82 1.4049  4     0.349 5.0926 0.001026 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The output here shows us on the basis of an F-test that we can reject H₀, so the more complex model in this case really is better at prediction, since p ≤ 0.05.

'Base R' scatter plots representing regression models

par(mfrow=c(1,2), mar=c(3,3,1,1), mgp=c(1.5,0.5,0), oma=c(0,0,0,0), tcl=0.2,
    cex=1.2, cex.lab=1.2, cex.axis=1., lend="square", ljoin="mitre", font.lab=2)
# simple scatterplot
plot(sv2017$Cr~sv2017$Fe, log="xy")
mtext(side=3, line=-1.2, text="(a)", adj=0.05, cex=1.4)
abline(lmCrFesimple, col=8, lty=2)
# grouped scatterplot
plot(sv2017$Cr~sv2017$Fe, log="xy", col=c(1,2,3)[sv2017$Type], pch=c(0,2,16)[sv2017$Type])
mtext(side=3, line=-1.2, text="(b)", adj=0.05, cex=1.4)
# use for() {...} loop to add individual regression lines
for (i in 1:NROW(levels(sv2017$Type))) {
abline(lm(log10(sv2017$Cr)~log10(sv2017$Fe),
          subset=sv2017$Type==levels(sv2017$Type)[i]), col=i, lty=2)
  }
legend("bottomright", legend=levels(sv2017$Type), col=c(1,2,3), pch=c(0,2,16),
       bty="n", inset=0.02)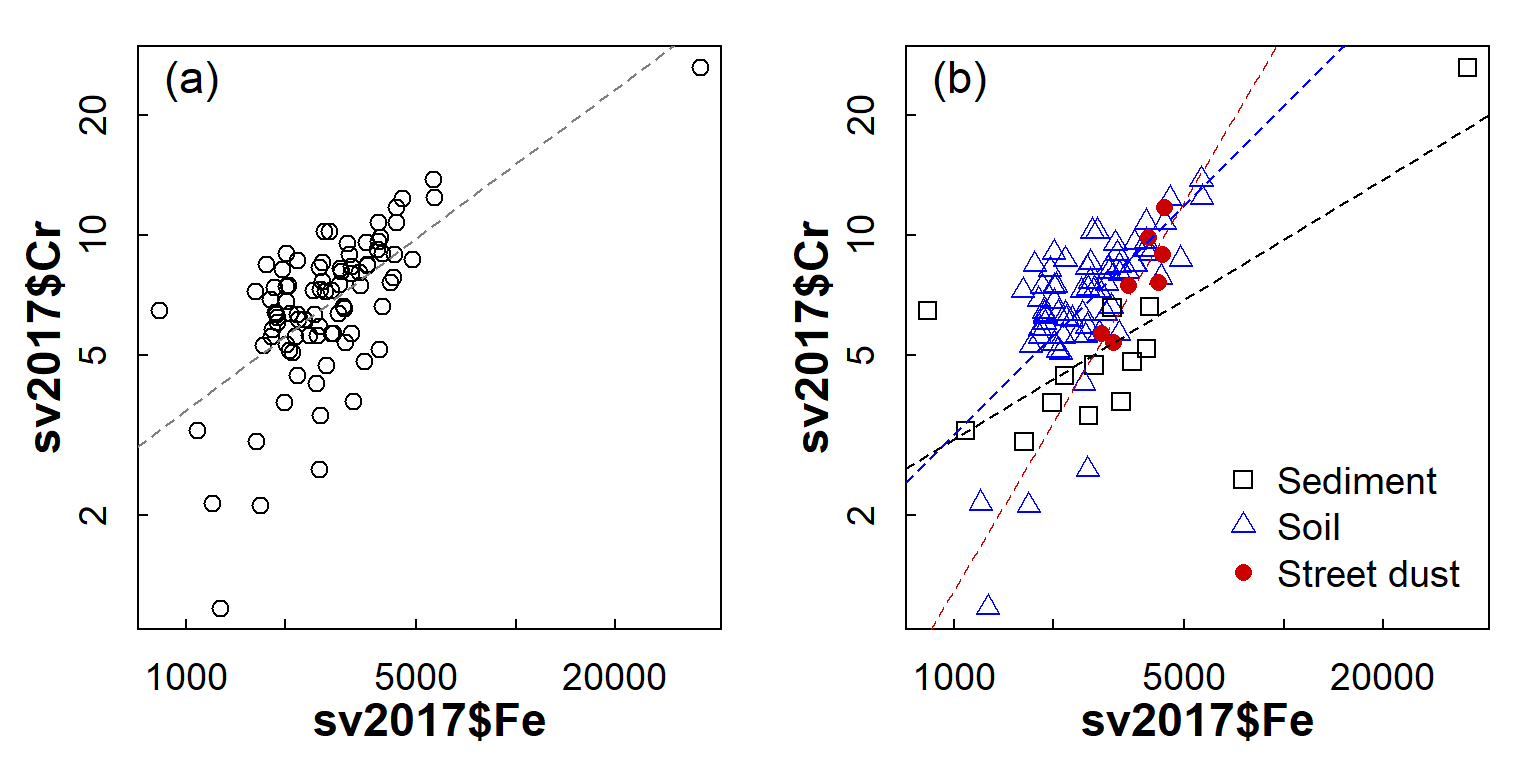

Figure 4: Scatterplot of Cr vs. Fe in the 2017 Smith's-Veryard data, showing (a) overall relationship and (b) relationship with observations grouped by sample Type.

On the basis of Figure 4, it seems likely that a grouped regression model (different slopes and intercepts for each sample Type) would better describe the Cr-Fe relationship, as the deviations from the model (the residuals) would be smaller overall.

"Begin challenging your own assumptions. Your assumptions are your windows on the world. Scrub them off every once in awhile, or the light won't come in."

--- Alan Alda

Diagnostic plots for regression

Simple linear regression, Cr ~ Fe

par(mfrow=c(2,2), mar=c(3,3,2,1))
plot(lmCrFesimple)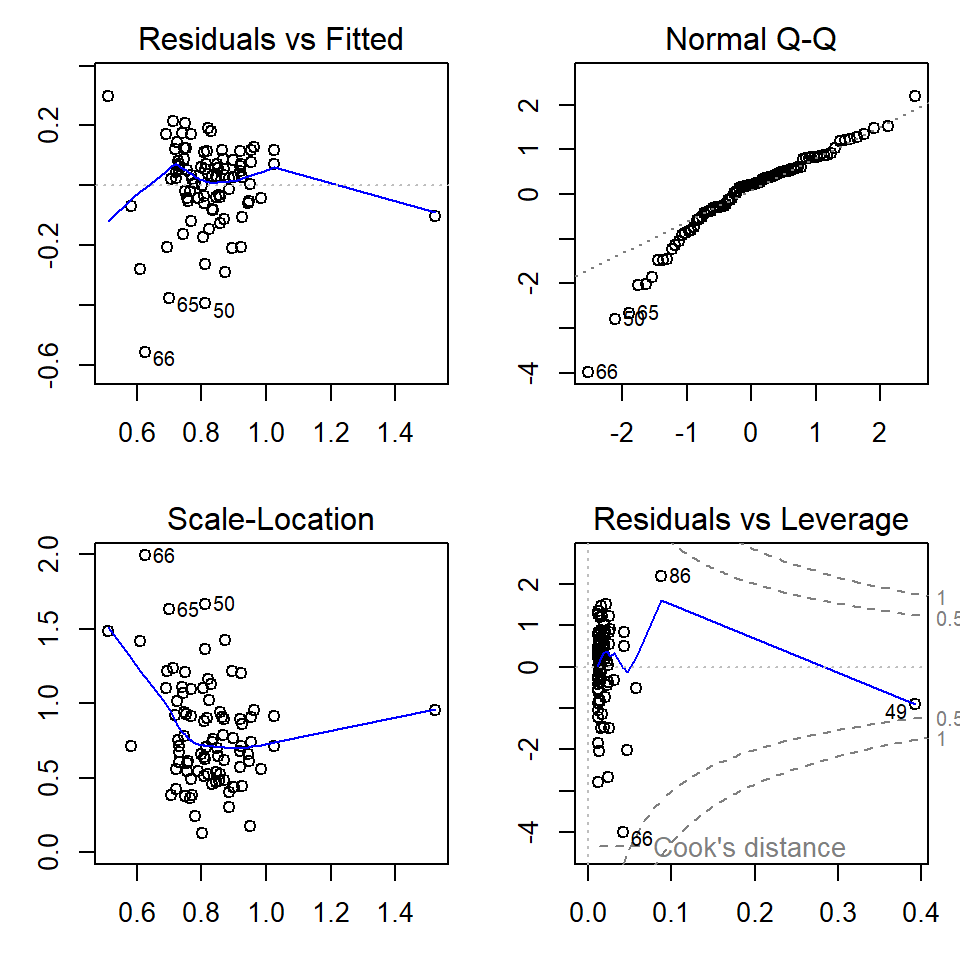

Figure 5: Regression diagnostic plots for Cr predicted from Fe using a simple linear regression model without grouping

par(mfrow=c(1,1), mar=c(3,3,1,1))

Grouped linear regression, Cr ~ Fe * Type

par(mfrow=c(2,2), mar=c(3,3,2,1))
plot(lmCrFe_byType)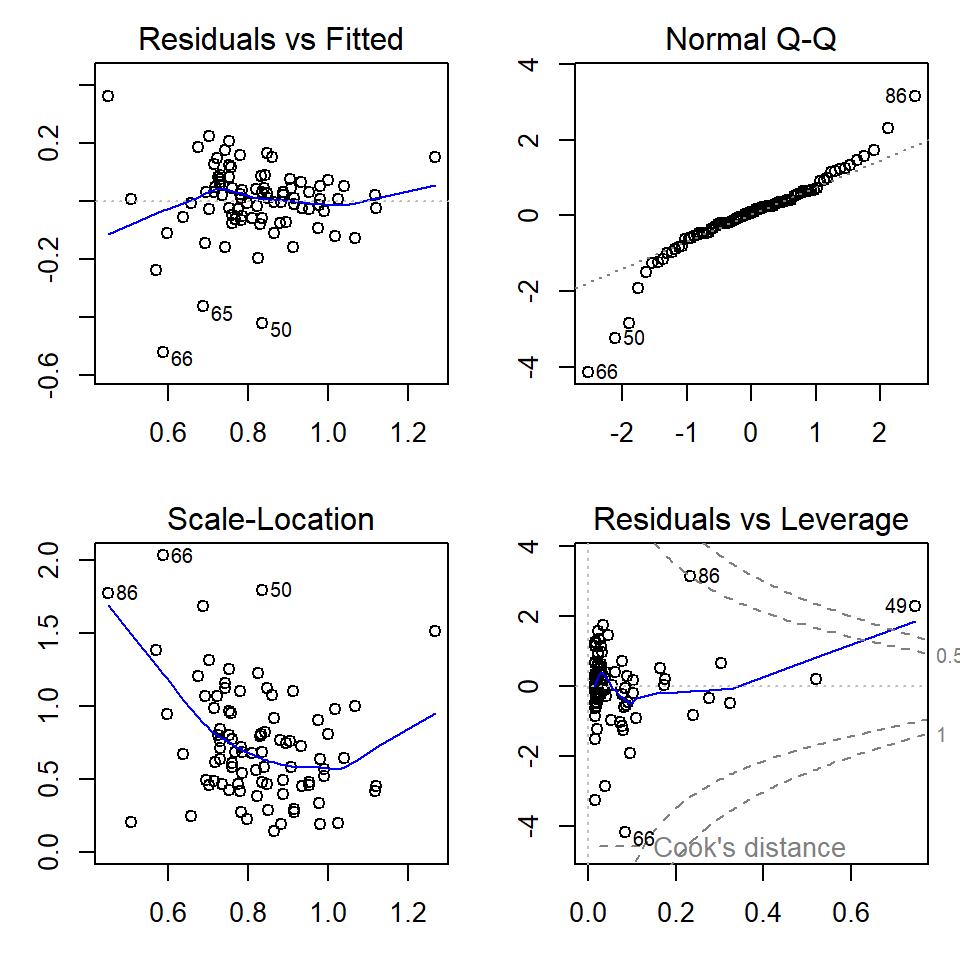

Figure 6: Regression diagnostic plots for Cr predicted from Fe using a grouped linear regression model with different parameters for each sample Type

par(mfrow=c(1,1), mar=c(3,3,1,1)) # change back to 1 plot at a time

The diagnostic plots (Figures 5 and 6) are a visual test of some of the assumptions of linear regression models, which relate mainly to the residuals.
[An alternative from the car package is influenceIndexPlot(yourModelName)].

The top left and bottom left plots in Figures 5 and 6 allow us to assess the assumption of homoscedasticity, that is, the residuals should be of similar absolute magnitude independent of the value of the dependent variable (actual or predicted). The top left plot also helps us to decide if the residuals are independent. In both the top left and bottom left plots, residuals should appear randomly distributed with a near-horizontal smoothed (blue) line.

The top right plot in Figures 5 and 6 is a Q-Q plot which tests another assumption of regression; that the residuals should be normally distributed. The points should lie along (or close to) the theoretical (dotted) line.

Finally the bottom left plot in Figures 5 and 6 tests whether any observations have an unusual influence on the regression statistics (the assumption is that they do not).

We can test all of these assumptions with formal statistical tests using the car and lmtest packages.

The Breusch-Godfrey test is for residual autocorrelation; H₀ is that residuals are not autocorrelated (i.e. observations probably independent)

require(lmtest)
bgtest(lmCrFe_byType) # autocorrelation (independence)

##
##  Breusch-Godfrey test for serial correlation of order up to 1
##
## data:  lmCrFe_byType
## LM test = 2.2568, df = 1, p-value = 0.133

The Breusch-Pagan test is for heteroscedasticity; H₀ is that residuals are homoscedastic (i.e. variance independent of value of variable).

bptest(lmCrFe_byType) # homoscedasticity

##
##  studentized Breusch-Pagan test
##
## data:  lmCrFe_byType
## BP = 12.407, df = 5, p-value = 0.02962

The Rainbow test is to test the assumption of linearity; H₀ is that the relationship is linear.

raintest(lmCrFe_byType) # linearity

##
##  Rainbow test
##
## data:  lmCrFe_byType
## Rain = 0.68614, df1 = 44, df2 = 38, p-value = 0.8859

The outlierTest() function in the car package implements the Bonferroni outlier test; H₀ is that all residuals are from the same population (i.e. no outliers). H₀ is tested with the Bonferroni (NOT unadjusted) p-value. If no Bonferroni p-value is≤ 0.05, so we cannot reject H₀, the function outputs the largest residual(s).

require(car)
outlierTest(lmCrFe_byType) # influential observations (outliers)

##     rstudent unadjusted p-value Bonferroni p
## 66 -4.633419         1.3569e-05    0.0011941

More things to try (Correlation & regression Week 1)

Try str(lm_object) and/or ls(lm_object) to see what is stored in regression results. You might be able to use the contents of a lm object to:

plot calculated values (from the regression model) vs. measured values
add a 1:1 relationship to the plot in 1. above
find out if any regression residuals are unusual
...and so on.

Steps in running a multiple regression model

Multiple regression models predict the value of one variable (the dependent variable) from two or more predictor variables (or just 'predictors'). They can be very useful in environmental science, but there are several steps we need to take to make sure
that we have a valid model.

In this example we're going to develop a regression model to predict copper (Cu) concentrations from several predictors. It makes sense to choose predictors that represent bulk soil properties that could plausibly control trace element concentrations. So, we choose variables like pH, EC, organic carbon, cation exchange capacity, and the major elements as predictors (but NOT other trace elements, as their concentrations are probably too low to control the concentration of anything else!)

Since we don't have organic carbon or cation exchange capacity in this dataset, and there are many missing values for EC, our initial predictors will be Al, Ca, Fe, K, Mg, Na, pH, and S. Both the predictors and dependent variable need to be appropriately transformed before we start!

Also, some of our initial predictors may be highly correlated (co-linear) with each other. In multiple regression, we don't want to include co-linear predictors, since then we'll have two (or more) predictors which effectively contain the same information – see below.

Read input data

sv2017 <- read.csv("sv2017_original.csv")
print(sv2017[1:5,2:11], row.names = FALSE)

##  Group Sample Type Easting Northing Longitude  Latitude   pH    EC   Al
##      1      1 Soil  391064  6466753  115.8476 -31.92992 7.14 215.1 2112
##      1      2 Soil  391074  6466745  115.8477 -31.92999 6.71 224.1 2136
##      1      3 Soil  391148  6466744  115.8485 -31.93001 5.99 143.0 2145
##      1      4 Soil  391134  6466729  115.8483 -31.93014 6.00 216.0 2375
##      1      5 Soil  391211  6466740  115.8492 -31.93005 5.91  74.3 2345

Assess collinearity between initial set of predictors

First we inspect the correlation matrix. It's useful to include the dependent variable as well, just to see which predictors are most closely correlated.

(We try to generate a 'tidier' table by restricting numbers to 3 significant digits, based on the smallest r value in each column. We don't need to use rcorr() or rcorr.adjust(), since we're not so interested in P-values for this purpose.)

Note that all variables are appropriately transformed!
You will need to do this yourself...

cor0 <-
  cor(sv2017[,c("Al.pow","Ca.pow","Fe.pow","K.log","Mg.log","Na.pow","pH","S.pow","Cu.pow")],
   use="pairwise.complete")
print(cor0,digits=3)

##        Al.pow    Ca.pow Fe.pow K.log Mg.log Na.pow     pH     S.pow Cu.pow
## Al.pow 1.0000  0.337147  0.666 0.497  0.340  0.398  0.281  0.052639  0.200
## Ca.pow 0.3371  1.000000  0.354 0.382  0.852  0.510  0.646 -0.000907  0.360
## Fe.pow 0.6656  0.353504  1.000 0.579  0.388  0.286  0.162  0.318639  0.620
## K.log  0.4974  0.381912  0.579 1.000  0.563  0.544  0.182  0.388158  0.351
## Mg.log 0.3396  0.851684  0.388 0.563  1.000  0.730  0.450  0.290523  0.458
## Na.pow 0.3982  0.510131  0.286 0.544  0.730  1.000  0.179  0.528523  0.273
## pH     0.2813  0.645961  0.162 0.182  0.450  0.179  1.000 -0.274046  0.149
## S.pow  0.0526 -0.000907  0.319 0.388  0.291  0.529 -0.274  1.000000  0.447
## Cu.pow 0.1997  0.360100  0.620 0.351  0.458  0.273  0.149  0.446677  1.000

rm(cor0)

The rule of thumb we use is that if predictor variables are correlated with Pearson's r ≥ 0.8 or r ≤ −0.8, then the collinearity is too large and one of the correlated predictors should be omitted. In the correlation table above this applies to the correlation between [transformed] Ca and Mg, with r=0.85. In this example we will run two versions of the model, one keeping both Ca and Mg, and one omitting Mg.

In either case, whether we run the model with or without omitting predictors, it's a good idea to calculate Variance Inflation Factors on the predictor variables in the model (see below) which can tell us if collinearity is a problem.

Generate multiple regression model for Cu (co-linear predictors NOT omitted)

We first delete any observations (rows) with missing (NA) values, otherwise when we reduce the number of predictors we may not have the same number of observations for all models, in which case we can't compare them.

# make new data object containing relevant variables with no missing values
sv2017_multreg <- na.omit(sv2017[c("Cu.pow","pH","Al.pow","Ca.pow","Fe.pow",
                                   "K.log","Mg.log","Na.pow","S.pow")])
# run model using correctly transformed variables
lm_multi <- lm(Cu.pow ~ pH + Al.pow + Ca.pow + Fe.pow + K.log + Mg.log +
               Na.pow + S.pow, data=sv2017_multreg)
summary(lm_multi)

##
## Call:
## lm(formula = Cu.pow ~ pH + Al.pow + Ca.pow + Fe.pow + K.log +
##     Mg.log + Na.pow + S.pow, data = sv2017_multreg)
##
## Residuals:
##      Min       1Q   Median       3Q      Max
## -0.19359 -0.06366 -0.01116  0.06602  0.26154
##
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.168281   0.436815  -0.385   0.7011
## pH           0.018789   0.017599   1.068   0.2890
## Al.pow      -0.005742   0.002674  -2.147   0.0349 *
## Ca.pow      -0.254957   0.508472  -0.501   0.6175
## Fe.pow      19.021831   3.391486   5.609 2.98e-07 ***
## K.log       -0.101394   0.061911  -1.638   0.1055
## Mg.log       0.205248   0.089255   2.300   0.0241 *
## Na.pow      -0.678065   0.503062  -1.348   0.1816
## S.pow        1.325708   0.504003   2.630   0.0103 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.09043 on 78 degrees of freedom
## Multiple R-squared:  0.5705, Adjusted R-squared:  0.5264
## F-statistic: 12.95 on 8 and 78 DF,  p-value: 1.098e-11

Note that the null hypothesis probability Pr(>|t|) for some predictors is ≤ 0.05, so we can't reject the null hypothesis – that this predictor has no effect on the dependent variable.

Calculate variance inflation factors (VIF) for the predictors in the 'maximal' model

To calculate variance inflation factors we use the function vif() from the car package. The input for vif() is a lm object (in this case lm_multi).

require(car)
{cat("Variance Inflation Factors\n")
vif(lm_multi)}

## Variance Inflation Factors
##       pH   Al.pow   Ca.pow   Fe.pow    K.log   Mg.log   Na.pow    S.pow
## 1.968627 2.333083 6.410154 2.486039 2.014962 7.272626 3.442307 2.302179

A general rule of thumb is that if VIF > 4 we need to do some further investigation, while serious multi-collinearity exists requiring correction if VIF > 10 (Hebbali, 2018). As we probably expected from the correlation coefficient (above), VIFs for both Ca and Mg are >4 in this model, which may be OK, but we will try a model which omits Ca or Mg (we'll choose Mg)...

Generate multiple regression model for Cu, omitting co-linear predictors

# make new data object containing relevant variables with no missing values
sv2017_multreg <- na.omit(sv2017[c("Cu.pow","pH","Al.pow","Ca.pow","Fe.pow",
                                   "K.log","Mg.log","Na.pow","S.pow")])
# run model using correctly transformed variables (omitting co-linear predictors)
lm_multi2 <- lm(Cu.pow ~ pH + Al.pow + Ca.pow + Fe.pow +
                  K.log + Na.pow + S.pow, data=sv2017_multreg)
summary(lm_multi2)

##
## Call:
## lm(formula = Cu.pow ~ pH + Al.pow + Ca.pow + Fe.pow + K.log +
##     Na.pow + S.pow, data = sv2017_multreg)
##
## Residuals:
##      Min       1Q   Median       3Q      Max
## -0.19308 -0.05483 -0.00613  0.05965  0.31834
##
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept)  0.627352   0.273779   2.291  0.02460 *
## pH           0.014878   0.017985   0.827  0.41058
## Al.pow      -0.006750   0.002709  -2.492  0.01481 *
## Ca.pow       0.628179   0.342172   1.836  0.07014 .
## Fe.pow      19.225647   3.481123   5.523 4.13e-07 ***
## K.log       -0.059303   0.060728  -0.977  0.33178
## Na.pow      -0.188612   0.468023  -0.403  0.68804
## S.pow        1.434614   0.515210   2.785  0.00671 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.09286 on 79 degrees of freedom
## Multiple R-squared:  0.5413, Adjusted R-squared:  0.5007
## F-statistic: 13.32 on 7 and 79 DF,  p-value: 3.18e-11

Note that again the null hypothesis probability Pr(>|t|) for some predictors is >0.05, so we can't reject the null hypothesis -- that this predictor has no effect on the dependent variable.

Calculate variance inflation factors (VIF) for the model omitting co-linear predictors

require(car)
{cat("Variance Inflation Factors\n")
vif(lm_multi2)}

## Variance Inflation Factors
##       pH   Al.pow   Ca.pow   Fe.pow    K.log   Na.pow    S.pow
## 1.950249 2.270458 2.753381 2.484341 1.838836 2.826085 2.281852

With the co-linear variable(s) omitted (on the basis of |Pearson's r| > 0.8), we now have no VIFs > 4. So we can move on to stepwise refinement of our [new] 'maximal' model...
[BUT note that in this case, with no VIF > 10, we could have simply skipped omitting Mg and moved on to the next step below.]

Stepwise refinement of maximal multiple regression model (omitting co-linear predictors)

We don't want to have too many predictors in our model -- just the predictors which explain significant proportions of the variance in our dependent variable. In addition, our data may be insufficient to generate a very complex model; one rule-of-thumb suggests 10-20 observations are needed to calculate coefficients for each predictor. Reimann et al. (2008) recommend that the number of observations should be at least 5 times the number of predictors. So, we use a systematic stepwise procedure to test variations of the model, which omits unnecessary predictors.

lm_stepwise <- step(lm_multi2, direction="both", trace=0)
summary(lm_stepwise)

##
## Call:
## lm(formula = Cu.pow ~ Al.pow + Ca.pow + Fe.pow + S.pow, data = sv2017_multreg)
##
## Residuals:
##      Min       1Q   Median       3Q      Max
## -0.19595 -0.06213 -0.01212  0.06451  0.31295
##
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)
## (Intercept)  0.624948   0.141354   4.421 2.99e-05 ***
## Al.pow      -0.007697   0.002343  -3.285  0.00150 **
## Ca.pow       0.644119   0.220434   2.922  0.00449 **
## Fe.pow      18.990226   2.975412   6.382 9.82e-09 ***
## S.pow        1.059291   0.366512   2.890  0.00493 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.09236 on 82 degrees of freedom
## Multiple R-squared:  0.529,  Adjusted R-squared:  0.506
## F-statistic: 23.02 on 4 and 82 DF,  p-value: 8.931e-13

require(car)
{cat("==== Variance Inflation Factors ====\n")
vif(lm_stepwise)}

## ==== Variance Inflation Factors ====

##   Al.pow   Ca.pow   Fe.pow    S.pow
## 1.716931 1.154967 1.834424 1.167152

In the optimised model, we find that the stepwise procedure has generated a new model with fewer predictor variables. You should notice that the p-values (Pr(>|t|)) for intercept and predictors are all now ≤ 0.05, so we can reject the null hypothesis for all predictors (i.e. none of them have 'no effect' on Cu). Our VIFs are now all close to 1, meaning negligible collinearity between predictors.

It's always a good idea to run diagnostic plots (see Figure 7 below) on a regression model (simple or multiple), to check for (i) any systematic trends in residuals, (ii) normally distributed residuals (or not), and (iii) any unusually influential observations.

Regression diagnostic plots

par(mfrow=c(2,2), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.6,0.5,0), font.lab=2, font.main=3,
    cex.main=0.8, tcl=-0.2)
plot(lm_stepwise)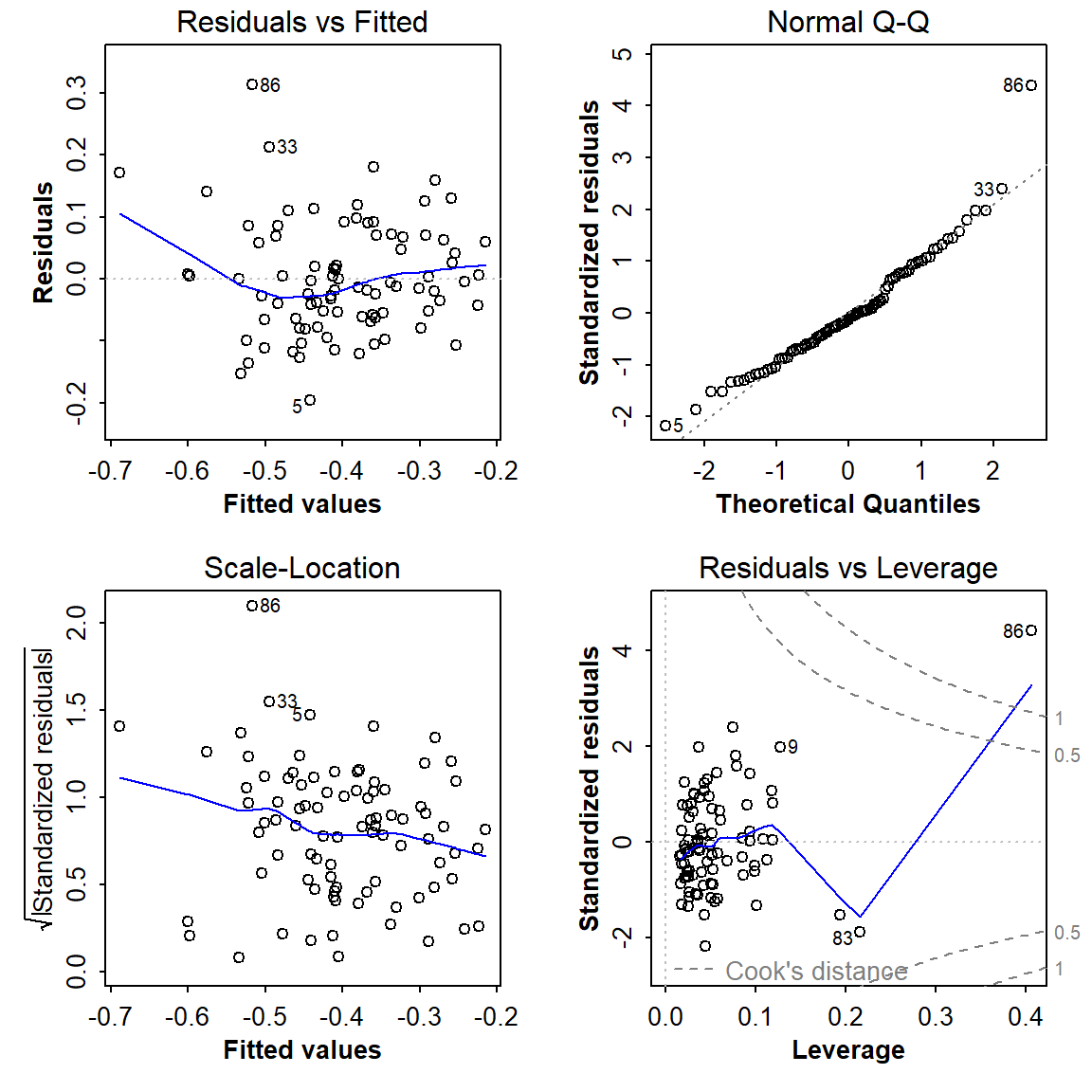

Figure 7: Diagnostic plots for the optimal multiple regression model following backward-forward stepwise refinement.

par(mfrow=c(1,1))

The optimal model is Cu.pow ~ Al.pow + Ca.pow + Fe.pow + S.pow, where suffixes .pow and .log represent power- and log₁₀-transformed variables respectively. The point labelled 86 does look problematic...

require(lmtest)
require(car)
cat("------- Residual autocorrelation (independence assumption):")
bgtest(lm_stepwise) # Breusch-Godfrey test for autocorrelation (independence)
cat("\n------- Test of homoscedasticity assumption:")
bptest(lm_stepwise) # Breusch-Pagan test for homoscedasticity
cat("\n------- Test of linearity assumption:")
raintest(lm_stepwise) # Rainbow test for linearity
cat("\n------- Bonferroni Outlier test for influential observations:\n\n")
outlierTest(lm_stepwise) # Bonferroni outlier test for influential observations

## ------- Residual autocorrelation (independence assumption):
##  Breusch-Godfrey test for serial correlation of order up to 1
##
## data:  lm_stepwise
## LM test = 2.8767, df = 1, p-value = 0.08987
##
##
## ------- Test of homoscedasticity assumption:
##  studentized Breusch-Pagan test
##
## data:  lm_stepwise
## BP = 27.533, df = 4, p-value = 1.551e-05
##
##
## ------- Test of linearity assumption:
##  Rainbow test
##
## data:  lm_stepwise
## Rain = 2.1033, df1 = 44, df2 = 38, p-value = 0.01057
##
##
## ------- Bonferroni Outlier test for influential observations:
##
##    rstudent unadjusted p-value Bonferroni p
## 86 5.002624         3.2263e-06   0.00028069

Multiple regression effect plots

require(effects)
plot(allEffects(lm_stepwise, confidence.level=0.95))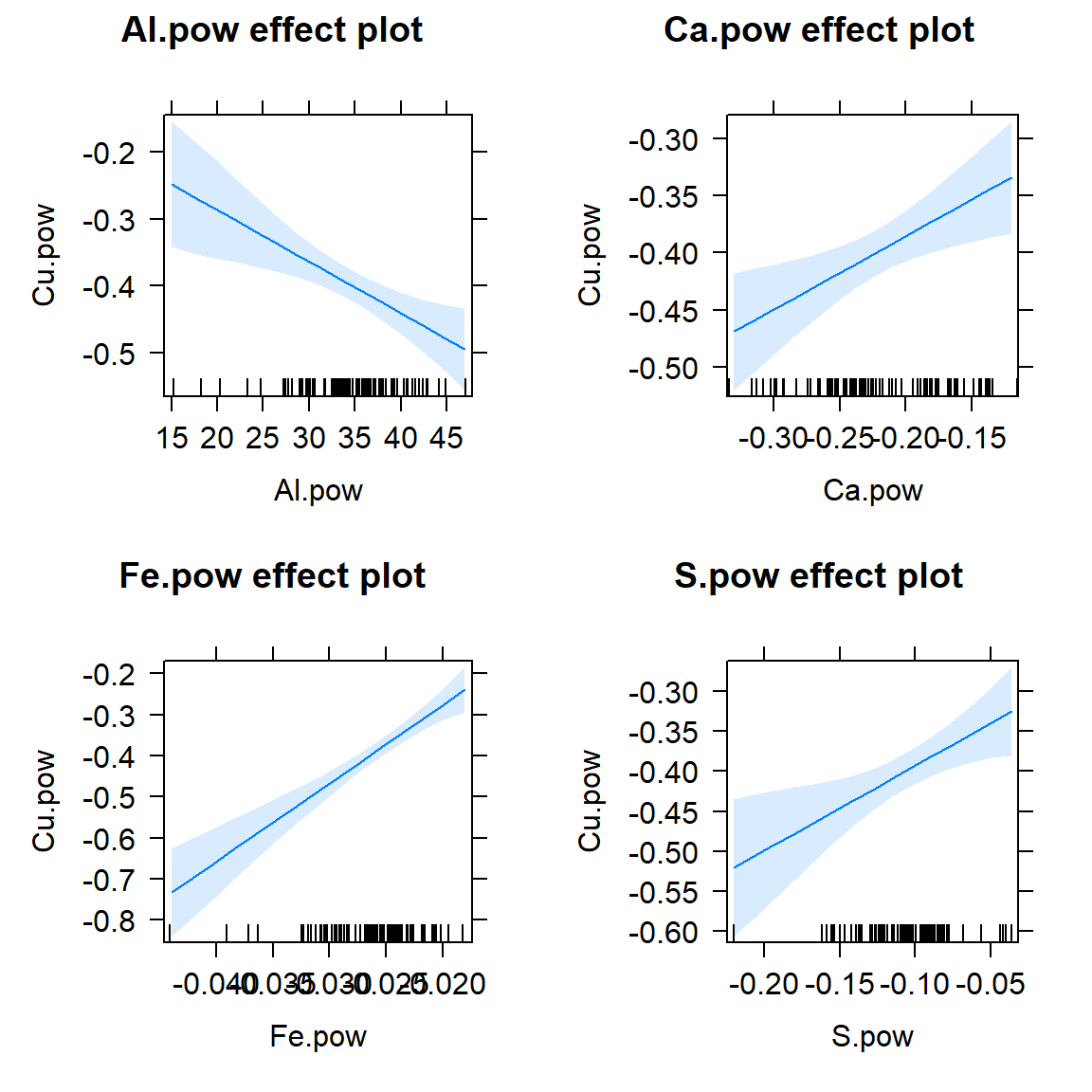

Figure 8: Effect plots for individual predictors in the optimal multiple regression model following backward-forward stepwise refinement. Light blue shaded areas on plots represent 95% confidence limits.

Scatterplot of observed vs. fitted values

An 'observed vs. fitted' plot (Figure 9) is a way around trying to plot a function with multiple predictors (i.e. multiple dimensions)! We can get the fitted values since these are stored in the lm object, in our case lm_stepwise in an item called lm_stepwise$fitted.values. We also make use of other information stored in the lm object, by calling summary(lm_stepwise)$adj.r.squared.

par(mar=c(4,4,1,1), mgp=c(2,0.5,0), font.lab=2, cex.lab=1.2,
    lend="square", ljoin="mitre")
plot(sv2017_multreg$Cu.pow ~ lm_stepwise$fitted.values,
     xlab="Cu.pow predicted from regression model",
     ylab="Cu.pow measured values", pch=3, lwd=2,
     cex=0.8, col="blue3")
abline(0,1, col="red", lty=2, lwd=2)
legend("topleft", legend=c("Observations","1:1 line"), col=c("blue3","red"),
       text.col=c("blue3","red"), pch=c(3,NA), lty=c(NA,2), pt.lwd=2, lwd=2,
       box.col="grey", box.lwd=2, inset=0.02, seg.len=2.7, y.intersp=1.2)
mtext(side=3, line=-5.5, adj=0.05, col="blue3",
      text=paste("Adjusted Rsq =",signif(summary(lm_stepwise)$adj.r.squared,3)))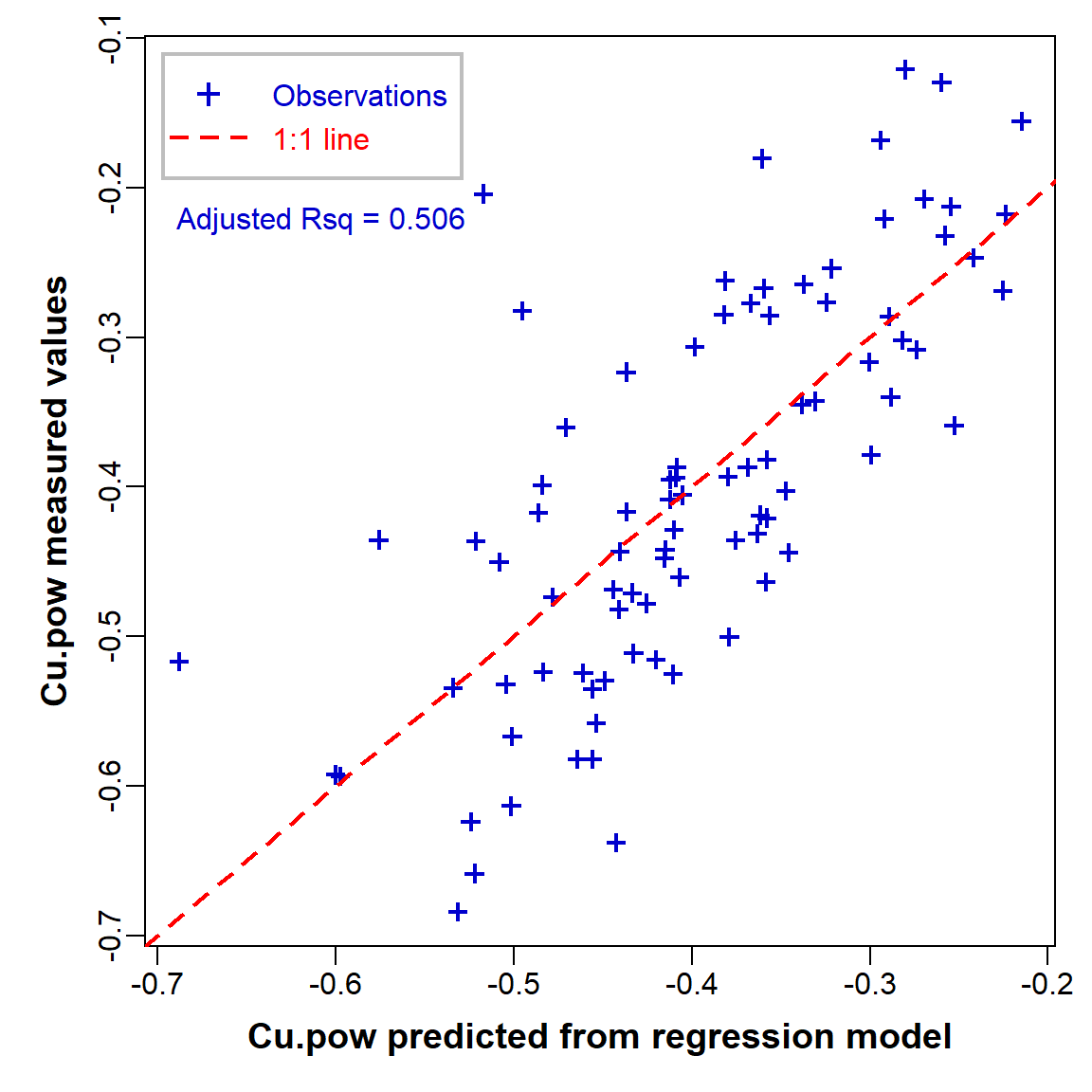

Figure 9: Measured (observed) vs. predicted values in the optimal multiple regression model.

Some brief interpretation

The adjusted R-squared value of the final model is 0.506, meaning that 50.6% of the variance in Cu is explained by variance in the model's predictors. (The remaining 49.4% of variance must therefore be due to random variations, or 'unknown' variables not included in our model.)
From the model coefficients and the effect plots we can see that Cu increases as Ca, Fe, and S increase, but Cu decreases as Al increases. This doesn't necessarily correspond with the individual relationships; Cu IS positively correlated with Ca, Fe, and S, but actually has no significant relationship with Al (you can check this!).
Although we can't attribute a causal relationship to correlation or regression relationships, the observed effects in our model are consistent with real phenomena. For example, copper is positively related to iron (Fe) in soils at the continental scale; see Hamon et al. (2004) and Caritat and Rate (2017).

References

Caritat, P. and Rate, A. W. (2017). Detecting anomalous metal concentrations in the regolith using cross-compositional detrending. Paper presented at the Goldschmidt Conference 2017, Paris, France. https://whiteiron.org/uploads/conferences/27/abstracts/finalPDFs/2017002103-20170327183746.pdf

Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences, Second Edition. Erlbaum Associates, Hillsdale, NJ, USA.

Hamon, R. E., McLaughlin, M. J., Gilkes, R. J., Rate, A. W., Zarcinas, B., Robertson, A., Cozens, G., Radford, N. and Bettenay, L. (2004). Geochemical indices allow estimation of heavy metal background concentrations in soils. Global Biogeochemical Cycles, 18(GB1014), http://dx.doi.org/10.1029/2003GB002063.

Hebbali, A. (2018). Collinearity Diagnostics, Model Fit and Variable Contribution. Vignette for R Package 'olsrr'. Retrieved 2018.04.05, from https://cran.r-project.org/web/packages/olsrr/vignettes/regression_diagnostics.html.

Reimann, C., Filzmoser, P., Garrett, R.G., Dutter, R., (2008). Statistical Data Analysis Explained: Applied Environmental Statistics with R. John Wiley & Sons, Chichester, England (see Chapter 16).

CC-BY-SA • All content by Ratey-AtUWA. My employer does not necessarily know about or endorse the content of this website.
Created with rmarkdown in RStudio using the cyborg theme from Bootswatch via the bslib package, and fontawesome v5 icons.

exploring relationships: correlation and regression