Principal Components Analysis for Compositional Data
| This follows on from the previous page which was an introduction to data with fixed-sum compositional closure. |
Before we start we need to read some data as before:
cities <-
read.csv(paste0("https://raw.githubusercontent.com/Ratey-AtUWA/",
"compositional_data/main/cities_Hu_etal_2021.csv"),
stringsAsFactors = TRUE)
row.names(cities) <- as.character(cities$City)We also need to use a log-ratio transform to remove compositional fixed-sum closure:
cities_clr <- cities
cities_clr[,2:5] <- t(apply(cities[,2:5], MARGIN = 1,
FUN = function(x){log(x) - mean(log(x))}))Principal components analysis
It is quite common to measure many variables in environmental science and other disciplines. Using various types of ordination analysis, we can use the information contained in multiple variables to create a reduced subset of variables containing nearly the same amount of information. Ordination methods are also referred to, for this reason, as 'data reduction' methods and are commonly used for multivariate analysis.
One of the earliest and most widely used ordination methods for exploration and dimension-reduction of multivariate data is principal components analysis (PCA). Imagine a dataset with many samples (rows) and n continuous numeric variables (columns) which contain quantitative information about each sample such as concentrations, heights, velocities, etc. For these n variables/dimensions, the principal component calculation generates n new variables, or principal components, which are each a function of the set of all the original variables (so each principal component is defined by a weighting or coefficient for each of the original variables). We may choose to omit some variables from the analysis if they contain too many missing observations or if there is another valid reason to doubt their integrity. Since each principal component is selected to account for successively smaller proportions of the multiple variance, it is usually the first few principal components which explain most of the variance and therefore contain the most useful information. We conventionally visualize this in a 'scree plot' (Figure 1), a kind of bar graph showing the decrease in variance accounted for by each component.
Base-R has two functions which perform Principal
Components Analysis (PCA). We will use the prcomp()
function which has better numerical accuracy and a more valid variance
calculation than the alternative princomp() (see
Details after running ?prcomp for more
information). We include the argument scale. = TRUE, as
this is better for avoiding unexpected results due to large differences
in magnitude of the variables.
#
data0 <- na.omit(cities[,c("Compact","Open","Lightweight","Industry")])
pca_cities_clos <- prcomp(data0, scale. = TRUE)
cat("Variable weightings (rotations) - closed data\n")
pca_cities_clos$rot
cat("...\n\nComponent Variances - Closed data\n")
pca_cities_clos$sdev^2
cat("...\n\nProportions of variance explained by each component",
"\nCLR-transformed (open) data\n")
round(pca_cities_clos$sdev^2/sum(pca_cities_clos$sdev^2),3)
cat("\n--------------------\nVariable weightings (rotations) - open data\n")
data0 <- na.omit(cities_clr[,c("Compact","Open","Lightweight","Industry")])
pca_cities_open <- prcomp(data0, scale. = TRUE)
pca_cities_open$rot
cat("...\n\nComponent Variances - CLR-transformed (open) data\n")
pca_cities_open$sdev^2
cat("...\n\nProportions of variance explained by each component",
"\nCLR-transformed (open) data\n")
round(pca_cities_open$sdev^2/sum(pca_cities_open$sdev^2),3)
rm(data0)## Variable weightings (rotations) - closed data
## PC1 PC2 PC3 PC4
## Compact -0.5582052 0.5356252 0.05639404 -0.63113567
## Open -0.3409659 -0.7576682 0.46899761 -0.29953715
## Lightweight 0.3992211 0.3417785 0.85067121 0.01297763
## Industry -0.6424731 0.1491041 0.23069343 0.71538580
## ...
##
## Component Variances - Closed data
## [1] 1.5860528 1.0026876 0.8705986 0.5406610
## ...
##
## Proportions of variance explained by each component
## CLR-transformed (open) data
## [1] 0.397 0.251 0.218 0.135
##
## --------------------
## Variable weightings (rotations) - open data
## PC1 PC2 PC3 PC4
## Compact -0.2081793 0.75498116 0.3214239 -0.5323077
## Open -0.3535490 -0.62668193 0.5577101 -0.4138022
## Lightweight 0.6833728 -0.17189496 -0.2520621 -0.6632635
## Industry -0.6038759 -0.08789385 -0.7225723 -0.3248042
## ...
##
## Component Variances - CLR-transformed (open) data
## [1] 1.975945e+00 1.511204e+00 5.128514e-01 1.470492e-31
## ...
##
## Proportions of variance explained by each component
## CLR-transformed (open) data
## [1] 0.494 0.378 0.128 0.000As we should expect, each component accounts for successively less variance. We can already see that removing closure has made a noticeable difference to the PCA output, both in the variable weightings and the component variances.
Principal Components Analysis output
As well as the component variances, the useful results of principal components analysis include the variable weightings or 'rotations' for each principal component. Referring to just the output for open data above, PC1 (which explains the most multivariate variance) has its greatest absolute contributions from the Lightweight and Industry variables, which act in opposite directions (remembering that the sign is arbitrary, but that relative sign and magnitude are important). PC2 contains mainly variance from the Compact and Open variables, PC3 (which explains much less variance) reflects Open/Industry, and we can ignore PC4 as it has a negligible component variance.
In addition, every individual observation (sample) is a multivariate point, the observation scores for all samples in each principal component based on the values of the variables used in PCA for that sample. It is conventional to plot both of these two types of output in a principal component biplot, as shown in Figure 2. Before discussing the biplot, we should note that the sign (positive or negative) of variable weightings and observation scores (i.e. the direction of the axes) is arbitrary and should not affect our interpretations.
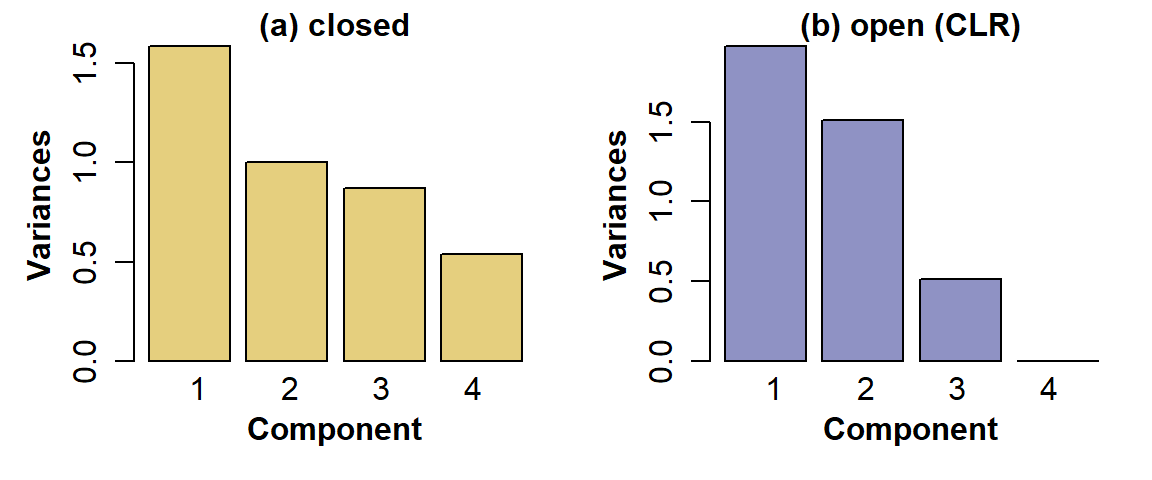
Figure 1: PCA scree plots for urban land-use data, for: (a) compositionally closed proportions; (b) data corrected for closure using CLR-transformation.
There are informal 'rules' for deciding which of the principal components contain useful information:
- Components having variance greater than 1 (the 'Kaiser' criterion)
- Components up to a cumulative proportion of variance explained of 0.8 (80%)
For example, for the open data, the component variances are PC1 1.976, PC2 1.511, PC3 0.513, PC4 1.5E-31 -- so only PC1 and PC2 meet the first criterion. Similarly, the cumulative proportions of variance explained by each component are PC1 0.494, PC1+PC2 0.872, so by criterion 2 no useful information is contained in principal components >2. In this example both criteria agree (they don't always!).
Another part of the PCA output that we need to know about is the set of observation scores, essentially showing where each observation (each city, in these data) plots in principal component space. We're only interested in PC1 and PC2, since they are the only components meeting the criteria. The observation scores for the first rows of the data are as follows (Table 1):
OScores <- data.frame(City=cities_clr$City[1:8],
PC1_closed=round(pca_cities_clos$x[1:8,1],3),
PC2_closed=round(pca_cities_clos$x[1:8,2],3),
PC1_open=round(pca_cities_open$x[1:8,1],3),
PC2_open=round(pca_cities_open$x[1:8,2],3))
flextable(OScores) |>
theme_zebra(odd_header = "#D0E0FF", even_header = "#D0E0FF") |>
border_outer(border = BorderDk, part = "all") |>
border_inner_v(border=BorderLt, part="header")City | PC1_closed | PC2_closed | PC1_open | PC2_open |
New York | -1.885 | -1.095 | -0.896 | 0.155 |
Sao Paulo | -2.054 | 0.732 | -0.646 | 0.722 |
Shanghai | -2.889 | -0.909 | -1.413 | -0.467 |
Beijing | -1.665 | -1.230 | -0.858 | 0.098 |
Jakarta | -2.515 | 2.528 | -0.592 | 2.491 |
Guangzhou | -2.679 | 1.453 | -1.099 | 0.957 |
Melbourne | -1.871 | 1.375 | -0.808 | 0.991 |
Paris | -0.632 | -2.171 | -0.615 | -0.489 |
Principal components biplots
require(car) # for data ellipses (see Fig 1.4)
palette(c("black",scico::scico(8, palette = "batlow", alpha = 0.7),"white"))
par(mfrow=c(1,2), mar = c(3.5,3.5,3.5,3.5), oma = c(0,0,0,0),
mgp=c(1.7,0.3,0), tcl = 0.25, font.lab=2,
lend = "square", ljoin = "mitre")
# choose components and set scaling factor (sf)
v1 <- 1; v2 <- 2; sf <- 0.4
biplot(pca_cities_clos, choices = c(v1,v2), col = c(2,1), cex=c(1,0.0),
pc.biplot = FALSE, scale = 0.4, arrow.len = 0.08,
xlim = c(-1.5,1.5), ylim = c(-1.5,1.5),
xlab = paste0("Scaled PC",v1," Component Loadings"),
ylab = paste0("Scaled PC",v2," Component Loadings"))
mtext(paste0("Scaled PC",v1," Observation Scores"), 3, 1.6, font = 2)
mtext(paste0("Scaled PC",v2," Observation Scores"), 4, 1.6, font = 2)
mtext("Untransformed data\n(compositionally closed)",
side = 3, line = -2, font = 2, adj = 0.98)
data0 <- na.omit(cities[,c("Type","Global","Region","Compact",
"Open","Lightweight","Industry")])
points(pca_cities_clos$x[,v1]*sf, pca_cities_clos$x[,v2]*sf*1.5,
pch = c(21:25)[data0$Type],
lwd = 1, bg = c(7,6,5,4,3)[data0$Type],
col = 1,
cex = c(1.4,1.3,1.2,1.2,1.2)[data0$Type])
dataEllipse(x=pca_cities_clos$x[,v1]*sf, y=pca_cities_clos$x[,v2]*sf*1.5,
groups = data0$Type, add = TRUE, plot.points = FALSE,
levels = c(0.9), center.pch = 3, col = c(2,3,8,9,11),
lty = 2, lwd = 1, center.cex = 2.4, group.labels = "")
legend("bottomright", bty = "o", inset = 0.03,
box.col = "gray", box.lwd = 2, bg = 10,
legend = levels(data0$Type),
pch = c(21:25), pt.lwd = 1,
col = 1, pt.bg = c(7,6,5,4,3),
pt.cex = c(1.4, 1.3, 1.2,1.2,1.2),
cex = 0.9, y.intersp = 0.9)
mtext("(a)", side = 3, line = -1.5, font = 2, adj = 0.02, cex = 1.25)
sf <- 0.25 # adjust scaling factor for next PCA biplot
biplot(pca_cities_open, choices = c(v1,v2), col = c(2,1), cex=c(0.8,1),
pc.biplot = FALSE, scale = 0.2, arrow.len = 0.08,
# xlim = c(-1.2,3.2), ylim = c(-3.5,1.7),
xlab = paste0("Scaled PC",v1," Component Loadings"),
ylab = paste0("Scaled PC",v2," Component Loadings"))
mtext(paste0("Scaled PC",v1," Observation Scores"), 3, 1.6, font = 2)
mtext(paste0("Scaled PC",v2," Observation Scores"), 4, 1.6, font = 2)
mtext("CLR\ntransformed\ndata\n(no closure)",
side = 3, line = -4, font = 2, adj = 0.98)
data0 <- na.omit(cities_clr[,c("Type","Compact","Open","Lightweight","Industry")])
points(pca_cities_open$x[,v1]*sf, pca_cities_open$x[,v2]*sf,
pch = c(21:25)[data0$Type],
lwd=2, bg = c(7,6,5,4,3)[data0$Type],
col = c(1,1,1,1,1)[data0$Type],
cex = c(1.4,1.3,1.2,1.2,1.2)[data0$Type])
dataEllipse(x=pca_cities_open$x[,v1]*sf, y=pca_cities_open$x[,v2]*sf*1.5,
groups = data0$Type, add = TRUE, plot.points = FALSE,
levels = c(0.9), center.pch = 3, col = c(7,6,5,4,3),
lty = 2, lwd = 2, center.cex = 2.4, group.labels = "")
legend("bottomright", bty = "o", inset = 0.03,
box.col = "gray", box.lwd = 2, bg = 10,
legend = levels(data0$Type),
pch = c(21:251), pt.lwd = 2,
col = 1, pt.bg = c(7,6,5,4,3),
pt.cex = c(1.4, 1.3, 1.2,1.2,1.2),
cex = 0.9, y.intersp = 0.9)
mtext("(b)", side = 3, line = -1.5, font = 2, adj = 0.02, cex = 1.25)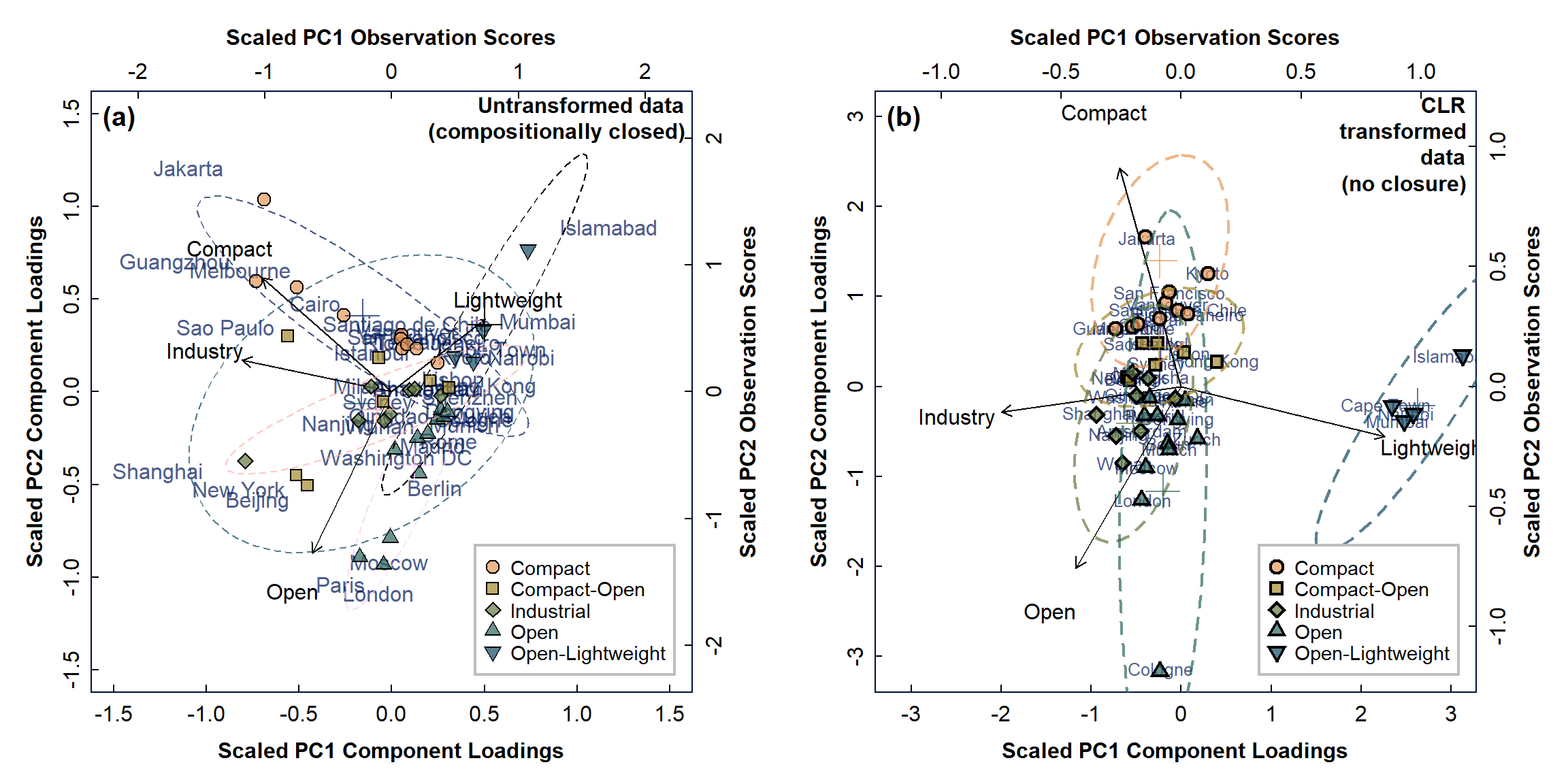
Figure 2: PCA biplots for urban land-use data, with observations categorised by type for: (a) compositionally closed proportions; (b) data corrected for closure using CLR-transformation.
PCA biplots are useful, because the variable weightings group together for variables (measurements) that are related to one another. For example, in the biplots in Figure 2, the variables are relative land areas under 4 land-use categories (which have been corrected in Figure 2(b) for compositional closure using the CLR transformation). These variables are shown as vectors (arrows) in the biplot of principal components PC1 and PC2, and variables which are related have vectors of similar length and/or direction. For example, the variables 'Compact' and 'Industry' plot closely together on biplot (a), suggesting some relationship between these land use categories. Removing closure in our data (biplot (b)) seems to remove this relationship, so it is probably not real!
Often we see the component vectors arranged in an obviously asymmetric pattern with closed data, and this is more apparent further down this page when we analyse some geochemical data. (When closure is removed, the vectors have a less asymmetric pattern - see Figure 4 below.)
The other main information we obtain from principal components biplots is from the observation scores (see above). These will plot at locations similar to their dominant variables: for example, in Figure 2(b), the 'Compact' cities all plot towards the top of the biplot in the same direction as the 'Compact' variable weighting vector. This suggests that compact cities have greater proportions of compact land use -- which should not be too surprising! Note that in the biplot for closed data in Figure 2(a), the separation of cities is not so clear.
Some other things to try
We could also group the observation scores in our biplot by a different factor in our dataset. For example, it would be interesting to see if we could observe any separation of cities by geographical region in the principal components analysis. You might want to practice your R coding on this problem!
Try some geochemical data
First we read and curate the data...
ashfield <-
read.csv(paste0("https://raw.githubusercontent.com/Ratey-AtUWA/",
"compositional_data/main/AFR_surfSed_2019-2021.csv"),
stringsAsFactors = TRUE)
ashfield$Year <- as.factor(ashfield$Year)...and then apply a CLR-transformation to remove closure for the relevant set of variables.
ashfield_clr <- ashfield
ashfield_clr[,11:38] <- t(apply(ashfield[,11:38], MARGIN = 1,
FUN = function(x){log(x) - mean(log(x), na.rm=TRUE)}))
head(ashfield_clr[,11:17])## Al As Ba Ca Cd Ce Co
## 1 4.915247 -2.629041 -0.9121439 4.363272 -5.860602 -1.7556753 -0.808294
## 2 5.485119 -3.237030 -0.8175805 3.059425 -5.505493 -0.5044887 -2.056470
## 3 5.453100 -3.673684 -0.8895440 3.585314 -6.701993 -0.4096881 -2.581503
## 4 5.510806 NA -0.3797352 3.032430 -7.305800 -0.5253843 -2.722609
## 5 5.601512 -2.808624 -0.6332189 3.276841 -7.804974 -0.3297310 -2.845259
## 6 5.774326 -3.398333 -0.5061159 3.665076 -8.188598 -0.3984539 -2.680560We run the PCA using prcomp() as before:
data0 <- na.omit(ashfield[,c(3,4,11:38)])
pca_ashfield_clos <- prcomp(data0[,3:30], scale. = TRUE)
cat("Variable weightings (rotations) - closed data (first 8 PCs, first 6 variables)\n")
head(pca_ashfield_clos$rot[,1:8])
cat("...\n\nComponent Variances - Closed data\n")
pca_ashfield_clos$sdev^2
cat("...\n\nProportions of variance explained by each component",
"\nuntransformed (closed) data\n")
round(pca_ashfield_clos$sdev^2/sum(pca_ashfield_clos$sdev^2),3)
cat("\nCumulative proportions of variance explained by each component",
"\nuntransformed (closed) data\n")
cumsum(round(pca_ashfield_clos$sdev^2/sum(pca_ashfield_clos$sdev^2),3))
cat("\n--------------------\nVariable weightings (rotations) - open data (first 8 PCs, first 6 variables)\n")
data0 <- na.omit(ashfield_clr[,c(3,4,11:38)])
pca_ashfield_open <- prcomp(data0[,3:30], scale. = TRUE)
head(pca_ashfield_open$rot[,1:8])
cat("...\n\nComponent Variances - CLR-transformed (open) data\n")
pca_ashfield_open$sdev^2
cat("...\n\nProportions of variance explained by each component",
"\nCLR-transformed (open) data\n")
round(pca_ashfield_open$sdev^2/sum(pca_ashfield_open$sdev^2),3)
cat("\nCumulative proportions of variance explained by each component",
"\nCLR-transformed (open) data\n")
cumsum(round(pca_ashfield_open$sdev^2/sum(pca_ashfield_open$sdev^2),3))## Variable weightings (rotations) - closed data (first 8 PCs, first 6 variables)
## PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8
## Al 0.26995403 0.02633354 -0.05476659 0.04780025 -0.170443860 0.01762888 -0.105268735 0.005053313
## As -0.06120107 0.33521218 0.33148706 -0.08779863 -0.096991015 -0.08263019 -0.008745784 0.129776759
## Ba 0.20427394 0.05736266 0.09020638 0.09714968 0.056301797 0.07914871 0.047941374 -0.629854958
## Ca -0.08330025 0.18449725 -0.21639305 0.35610423 0.086945376 0.27137437 0.120807867 0.097251199
## Cd -0.06798877 0.33587682 0.04719530 -0.11114968 -0.391415304 0.05597947 -0.028930259 0.107731197
## Ce 0.27232654 -0.02564881 0.06108687 0.21857702 -0.006019266 -0.12734748 0.099923015 0.139295484
## ...
##
## Component Variances - Closed data
## [1] 11.136553574 4.065487656 2.666708930 1.986894482 1.546288044 1.456684747 0.928308160 0.775284072
## [9] 0.707392079 0.560782892 0.383045806 0.332962097 0.316925599 0.216540483 0.180900583 0.162371080
## [17] 0.129129167 0.097760183 0.089066382 0.061632112 0.060339567 0.052328411 0.033538748 0.025822684
## [25] 0.018869847 0.005555844 0.001721885 0.001104884
## ...
##
## Proportions of variance explained by each component
## untransformed (closed) data
## [1] 0.398 0.145 0.095 0.071 0.055 0.052 0.033 0.028 0.025 0.020 0.014 0.012 0.011 0.008 0.006 0.006 0.005 0.003
## [19] 0.003 0.002 0.002 0.002 0.001 0.001 0.001 0.000 0.000 0.000
##
## Cumulative proportions of variance explained by each component
## untransformed (closed) data
## [1] 0.398 0.543 0.638 0.709 0.764 0.816 0.849 0.877 0.902 0.922 0.936 0.948 0.959 0.967 0.973 0.979 0.984 0.987
## [19] 0.990 0.992 0.994 0.996 0.997 0.998 0.999 0.999 0.999 0.999
##
## --------------------
## Variable weightings (rotations) - open data (first 8 PCs, first 6 variables)
## PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8
## Al 0.2178761 -0.175508744 0.110495240 -0.06970021 0.07015334 -0.02101289 0.20442617 -0.1993189
## As -0.2047095 -0.181257338 -0.202507482 0.10924893 0.10719031 -0.11524954 -0.08703576 -0.2380530
## Ba 0.1050193 -0.150214445 -0.047486395 -0.02175757 -0.14850985 -0.61186474 0.39012320 0.4123293
## Ca -0.1738396 0.045453704 0.199087874 -0.28077341 -0.06087187 -0.18134128 -0.09351070 -0.5848205
## Cd -0.2318630 -0.144853181 0.008502368 0.02861680 0.07265346 0.22920487 -0.04565633 0.2309725
## Ce 0.2627008 -0.002588997 -0.144448507 -0.17814957 0.16699334 0.04285596 -0.05901182 0.0236751
## ...
##
## Component Variances - CLR-transformed (open) data
## [1] 1.165706e+01 3.619179e+00 2.753411e+00 2.339868e+00 1.638357e+00 1.240181e+00 8.625783e-01 6.309300e-01
## [9] 5.935636e-01 4.648664e-01 4.266296e-01 2.947315e-01 2.784008e-01 2.291795e-01 1.888286e-01 1.552614e-01
## [17] 1.497596e-01 1.258552e-01 9.168352e-02 7.637244e-02 5.451782e-02 3.796124e-02 3.090203e-02 2.757347e-02
## [25] 2.237504e-02 8.676022e-03 1.298201e-03 2.931132e-30
## ...
##
## Proportions of variance explained by each component
## CLR-transformed (open) data
## [1] 0.416 0.129 0.098 0.084 0.059 0.044 0.031 0.023 0.021 0.017 0.015 0.011 0.010 0.008 0.007 0.006 0.005 0.004
## [19] 0.003 0.003 0.002 0.001 0.001 0.001 0.001 0.000 0.000 0.000
##
## Cumulative proportions of variance explained by each component
## CLR-transformed (open) data
## [1] 0.416 0.545 0.643 0.727 0.786 0.830 0.861 0.884 0.905 0.922 0.937 0.948 0.958 0.966 0.973 0.979 0.984 0.988
## [19] 0.991 0.994 0.996 0.997 0.998 0.999 1.000 1.000 1.000 1.000For both the closed and open data, we reach 80% of variance explained by component 6.
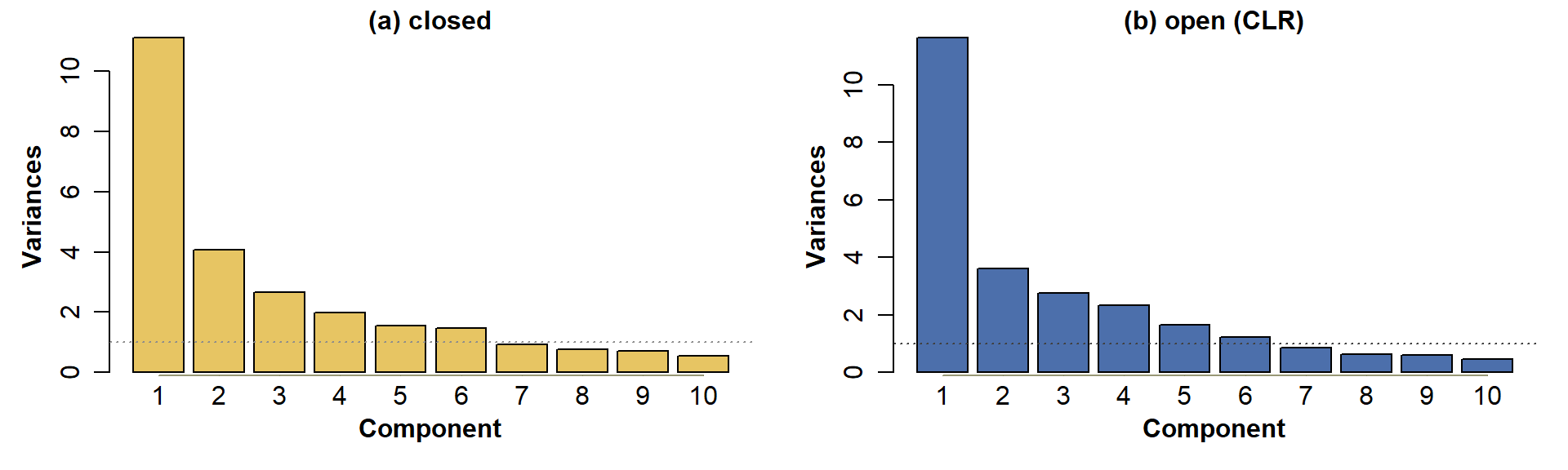
Figure 3: PCA scree plots for Ashfield data, for: (a) compositionally closed proportions; (b) data corrected for closure using CLR-transformation.
Figure 3 shows that for this analysis, 7 components have variances > 1, regardless of closure.
OScores <- data.frame(Samp=ashfield_clr$SampID[1:8],
PC1_closed=round(pca_ashfield_clos$x[1:8,1],3),
PC2_closed=round(pca_ashfield_clos$x[1:8,2],3),
PC1_open=round(pca_ashfield_open$x[1:8,1],3),
PC2_open=round(pca_ashfield_open$x[1:8,2],3))
flextable(OScores) |>
theme_zebra(odd_header = "#D0E0FF", even_header = "#D0E0FF") |>
border_outer(border = BorderDk, part = "all") |>
border_inner_v(border=BorderLt, part="header") |>
set_caption(caption="Table 2: PCA observation scores for the first 8 rows of the Ashfield Flats data (closed and open)")Samp | PC1_closed | PC2_closed | PC1_open | PC2_open |
2019_1_1 | -5.603 | 1.077 | -7.490 | 4.090 |
2019_1_2 | 1.907 | 1.272 | -0.544 | 1.529 |
2019_1_3 | 1.251 | 0.397 | 0.637 | 2.714 |
2019_1_4 | 1.272 | 0.390 | 1.237 | 1.460 |
2019_1_5 | 1.127 | -0.293 | 1.819 | 2.410 |
2019_1_6 | 0.839 | 0.993 | 0.087 | 2.629 |
2019_1_7 | 0.483 | 0.175 | 0.877 | 3.000 |
2019_1_8 | -0.547 | 4.114 | -3.505 | 2.875 |
par(mfrow=c(1,2), mar = c(3.5,3.5,3.5,3.5), oma = c(0,0,0,0),
mgp=c(1.7,0.3,0), tcl = 0.25, font.lab=2,
lend = "square", ljoin = "mitre")
# choose components and set scaling factor (sf)
v1 <- 1; v2 <- 2; sf <- 0.12
biplot(pca_ashfield_clos, choices = c(v1,v2), col = c("#ffffff00",1), cex=c(1,0.0),
pc.biplot = FALSE, scale = 0.4, arrow.len = 0.08,
# xlim = c(-1.5,1.5), ylim = c(-1.2,1.2),
xlab = paste0("Scaled PC",v1," Component Loadings"),
ylab = paste0("Scaled PC",v2," Component Loadings"))
mtext(paste0("Scaled PC",v1," Observation Scores"), 3, 1.6, font = 2)
mtext(paste0("Scaled PC",v2," Observation Scores"), 4, 1.6, font = 2)
mtext("Untransformed data\n(compositionally closed)",
side = 1, line = -2, font = 2, adj = 0.04)
data0 <- na.omit(ashfield[,c(3,4,9:38)])
points(pca_ashfield_clos$x[,v1]*sf, pca_ashfield_clos$x[,v2]*sf*1.5,
pch = c(22,21,24)[data0$Type],
lwd = 1, bg = c(6,4,1)[data0$Type],
col = 1,
cex = c(1.2,1.4,1)[data0$Type])
legend("bottomright", bty = "o", inset = 0.03,
box.col = "gray", box.lwd = 2, bg = 10,
legend = levels(data0$Type),
pch = c(22,21,24), pt.lwd = 1
,
col = 1, pt.bg = c(6,4,1),
pt.cex = c(1.2, 1.4, 1),
cex = 0.9, y.intersp = 0.9)
mtext("(a)", side = 3, line = -1.5, font = 2, adj = 0.02, cex = 1.25)
sf <- 0.115 # adjust scaling factor for next PCA biplot
biplot(pca_ashfield_open, choices = c(v1,v2), col = c("transparent",1), cex=c(0.8,1),
pc.biplot = FALSE, scale = 0.2, arrow.len = 0.08,
# xlim = c(-1.2,3.2), ylim = c(-3.5,1.7),
xlab = paste0("Scaled PC",v1," Component Loadings"),
ylab = paste0("Scaled PC",v2," Component Loadings"))
mtext(paste0("Scaled PC",v1," Observation Scores"), 3, 1.6, font = 2)
mtext(paste0("Scaled PC",v2," Observation Scores"), 4, 1.6, font = 2)
mtext("CLR-transformed\ndata (no closure)",
side = 1, line = -2, font = 2, adj = 0.04)
data0 <- na.omit(ashfield_clr[,c(3,4,9:38)])
points(pca_ashfield_open$x[,v1]*sf, pca_ashfield_open$x[,v2]*sf,
pch = c(22,21,24)[data0$Type],
lwd = 1, bg = c(6,4,1)[data0$Type],
col = 1,
cex = c(1.2,1.4,1)[data0$Type])
legend("bottomright", bty = "o", inset = 0.03,
box.col = "gray", box.lwd = 2, bg = 10,
legend = levels(data0$Type),
pch = c(22,21,24), pt.lwd = 1,
col = 1, pt.bg = c(6,4,1),
pt.cex = c(1.2, 1.4, 1),
cex = 0.9, y.intersp = 0.9)
mtext("(b)", side = 3, line = -1.5, font = 2, adj = 0.02, cex = 1.25)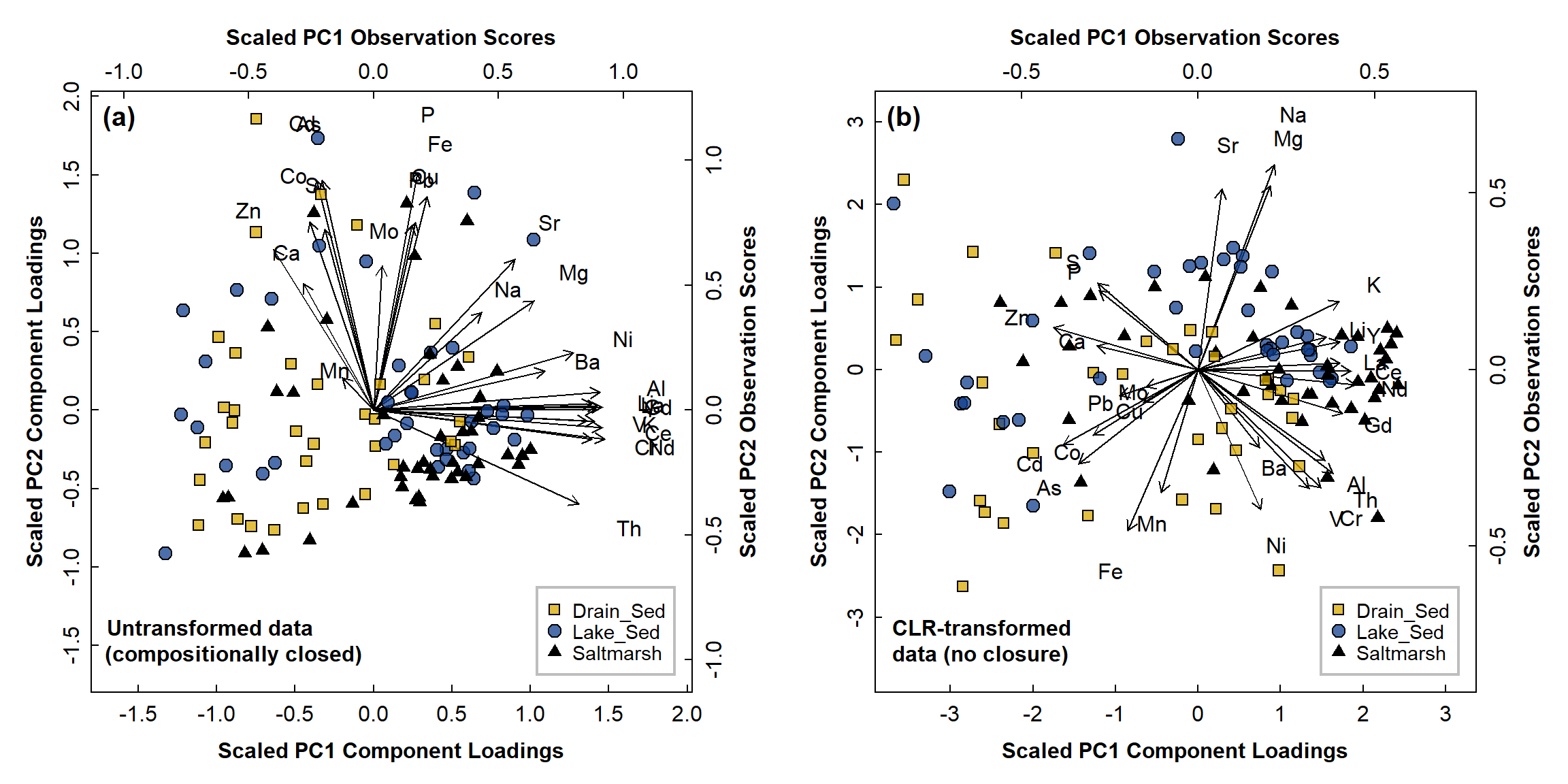
Figure 4: PCA biplots for Ashfield data, with observations categorised by sample type for: (a) compositionally closed proportions; (b) data corrected for closure using CLR-transformation.
We can see some interesting effects in Figure 4:
- there is obvious asymmetry in the biplot for the closed data (Figure 4(a)) which can make any effects hard to interpret, even if they were valid
- in the biplot for open (clr-transformed) data (Figure 4(b)), some of the elemental associations make sense (e.g. Sr-Na-Mg, the REEs Ce-La-Nd-Gd-(Y), redox-sensitive elements Fe-Mn, etc.)
- some clustering of observations is apparent in Figure 4(b), e.g. some Saltmarsh sediments seem to be associated with high REE concentrations; drain sediments are mainly towards the lower left
We might see clearer groupings based on a different factor.
| This followed on from the previous page which was an introduction to data with fixed-sum compositional closure. |
References and R Packages
Fox, J. (2022). RcmdrMisc: R Commander Miscellaneous Functions. R package version 2.7-2. https://CRAN.R-project.org/package=RcmdrMisc
John Fox and Sanford Weisberg (2019). An {R} Companion to Applied Regression (car), Third Edition. Thousand Oaks CA: Sage. URL: https://socialsciences.mcmaster.ca/jfox/Books/Companion/
Garrett, R.G. (2018). rgr: Applied Geochemistry EDA. R package version 1.1.15. https://CRAN.R-project.org/package=rgr
Hu, J., Wang, Y., Taubenböck, H., Zhu, X.X. (2021). Land consumption in cities: A comparative study across the globe. Cities, 113: 103163, https://doi.org/10.1016/j.cities.2021.103163.
Kassambara, A. and Mundt, F. (2020). factoextra: Extract and Visualize the Results of Multivariate Data Analyses. R package version 1.0.7. https://CRAN.R-project.org/package=factoextra
Maechler, M., Rousseeuw, P., Struyf, A., Hubert, M., Hornik, K.(2021). cluster: Cluster Analysis Basics and Extensions. R package version 2.1.2. https://CRAN.R-project.org/package=cluster
Reimann, C., Filzmoser, P., Garrett, R. G., & Dutter, R. (2008). Statistical Data Analysis Explained: Applied Environmental Statistics with R (First ed.). John Wiley & Sons, Chichester, UK.
Venables, W. N. & Ripley, B. D. (2002) Modern Applied Statistics with S (MASS). Fourth Edition. Springer, New York. ISBN 0-387-95457-0. http://www.stats.ox.ac.uk/pub/MASS4/
Wickham, H. (2019). stringr: Simple, Consistent Wrappers for Common String Operations. R package version 1.4.0. https://CRAN.R-project.org/package=stringr
Xu, N., Rate, A. W., & Morgan, B. (2018). From source to sink: Rare-earth elements trace the legacy of sulfuric dredge spoils on estuarine sediments. Science of The Total Environment, 637-638, 1537-1549. https://doi.org/10.1016/j.scitotenv.2018.04.398
CC-BY-SA • All content by Ratey-AtUWA. My employer does not necessarily know about or endorse the content of this website.
Created with rmarkdown in RStudio using the cyborg theme from Bootswatch via the bslib package, and fontawesome v5 icons.