Statistics for Comparing Means

See also my other GitHub Pages website dedicated to teaching: “R for Environmental Science”.

Intro: Comparisons of means between groups

Comparison of means tests help you determine whether or not your groups of observations have similar means. The groups are defined by the value of a factor (a categorical variable) for each row (observation) of our dataset.

There are many cases in statistics where you'll want to compare means for two or more populations, samples, or sample types. The parametric tests like t-tests or ANOVA compare the variance between groups with the variance within groups, and use the relative sizes of these 2 variances to estimate the probability that means are different.

The parametric mean comparison tests require the variables to have normal distributions. We also often assume that all groups of observations have
equal variance in the variable being compared. If the variances in each group are not similar enough (i.e. the variable is heteroskedastic), we need to modify or change the statistical test we use.

Means comparisons based on Null Hypothesis Statistical Testing (NHST) compare the variance between groups with the variance within groups, and generate a statistic which, if large/unlikely enough (i.e. p =< 0.05), allows rejection of the null hypothesis (H₀ = no difference between means in each/all groups).

[Further down in this R Code Examples session, we'll look at 'non-parametric' ways of comparing means, to be used when our variable(s) don't meet all of the requirements of conventional (parametric) statistical tests.]

In this session we're going to use the 2017 Smith's Lake -- Charles Veryard Reserves dataset (see Figure 1) to compare means between groups for factors having:

only two groups (using only the soil data);
more than two groups (using the whole dataset).

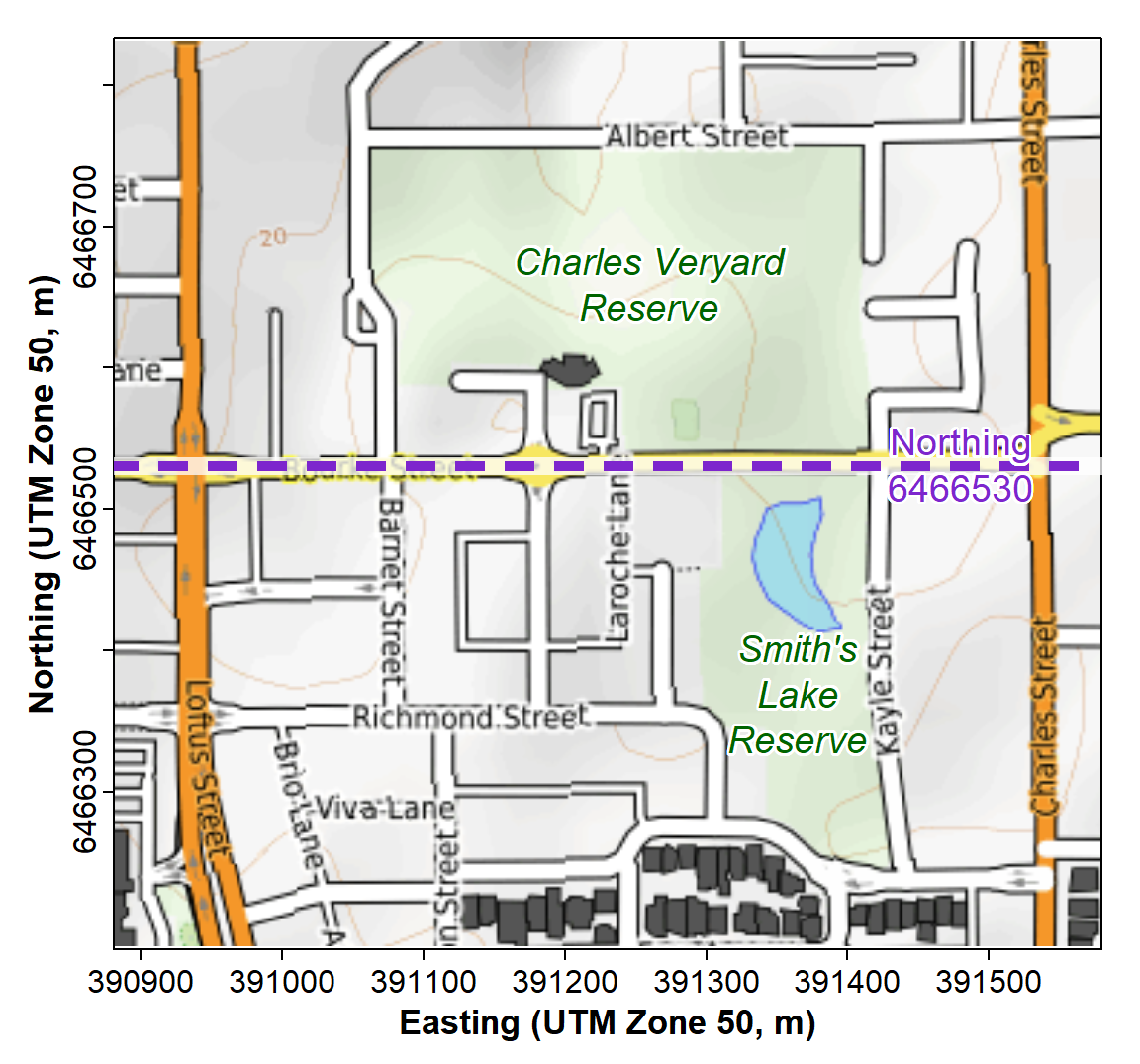
Figure 1: Map showing locations of Charles Veryard and Smiths Lake Reserves, North Perth, Western Australia.

Create a factor separating the two Reserves into groups AND limit the data to only soil

We split the dataset at Northing = 6466530 m, which represents Bourke Street.

require(car)
sv2017$Reserve <- cut(sv2017$Northing,
                      breaks = c(0,6466530,9999999),
                      labels = c("Smiths","Veryard"))
sv17_soil <- subset(sv2017, subset=sv2017$Type=="Soil")
cat("Number of soil samples in each reserve\n"); summary(sv17_soil$Reserve)

## Number of soil samples in each reserve

##  Smiths Veryard
##      21      52

Check the newly-created factor with a plot

par(mfrow=c(1,1), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.6,0.25,0),
    font.lab=2, font.main=3, cex.main=1, tcl=0.3)
plot(sv17_soil$Northing~sv17_soil$Easting,
     pch = c(1,2)[sv17_soil$Reserve],
     col = c(2,4)[sv17_soil$Reserve],
     cex = c(1.25,1)[sv17_soil$Reserve],
     lwd = 2, asp=1, xlab="Easting (UTM Zone 50, m)",
     ylab="Northing (UTM Zone 50, m)", cex.axis=0.85, cex.lab=0.9,
     main = "Samples by reserve")
abline(h = 6466530, lty=2, col="gray")
legend("bottomleft", legend = c("Smiths Lake","Charles Veryard"),
       cex = 1, pch = c(1,2), col = c(2,4),
       pt.lwd = 2, pt.cex = c(1.25, 1), title = "Reserve",
       bty = "n", inset = 0.02)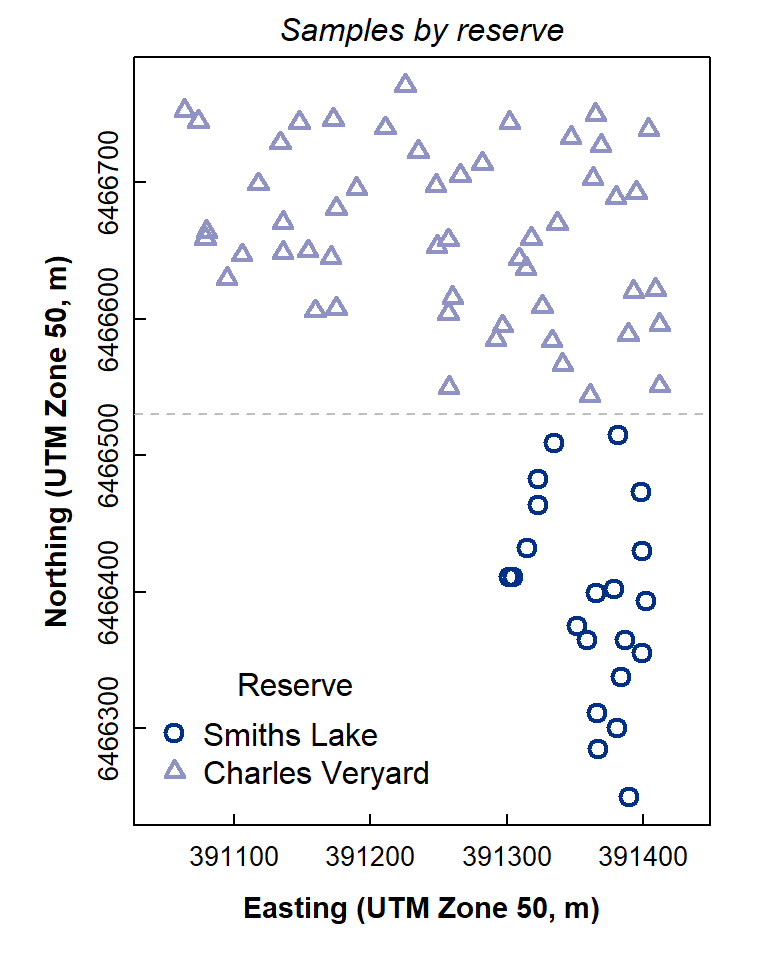

Figure 2: Location map of soil samples at Charles Veryard and Smiths Lake Reserves.

The plot in Figure 2 looks OK! You may have just made your first R map!

"...we have our work to do
Just think about the average..."

--- Rush, from the song 2112 (The Temples of Syrinx)

Means comparisons for exactly two groups

For variables which are normally distributed, we can use conventional, parametric statistics. The following example applies a t-test to compare mean values between Reserve. By default the R function t.test() uses the Welch t-test, which doesn't require the variance in each group to be equal (i.e., the Welch t-test is OK for heteroskedastic variables).
Of course, we still need to use appropriately transformed variables!

require(car)
powerTransform(sv17_soil$Na)

## Estimated transformation parameter
## sv17_soil$Na
##    0.1266407

sv17_soil$Na.pow <- (sv17_soil$Na)^0.127
t.test(sv17_soil$Na.pow ~ sv17_soil$Reserve)

##
##  Welch Two Sample t-test
##
## data:  sv17_soil$Na.pow by sv17_soil$Reserve
## t = -2.2869, df = 20.851, p-value = 0.03277
## alternative hypothesis: true difference in means between group Smiths and group Veryard is not equal to 0
## 95 percent confidence interval:
##  -0.166413933 -0.007862766
## sample estimates:
##  mean in group Smiths mean in group Veryard
##              1.762519              1.849657

We can visualize means comparisons in a few different ways – see Figure 3. My favourite is the boxplot with means included as extra information - with a bit of additional coding we can include the 95% confidence intervals as well! (but this is not shown in this document).

Visualising differences in means - 2 groups

par(mfrow=c(1,3), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.7,0.3,0),
    font.lab=2, font.main=3, cex.main=1, tcl=0.3,
    cex.lab = 1.4, cex.axis = 1.4)
boxplot(sv17_soil$Na.pow ~ sv17_soil$Reserve,
        notch=F, col="grey92",
        xlab="Reserve", ylab="Na (power-transformed)")
mtext("(a)", 3, -1.5, adj=0.03, font=2)
require(RcmdrMisc)
plotMeans(sv17_soil$Na.pow, sv17_soil$Reserve, error.bars="conf.int",
        xlab="Reserve", ylab="Na (power-transformed)",
        main = "Don't include plot titles for reports!")
mtext("(b)", 3, -1.5, adj=0.03, font=2)
#
# the third plot is a box plot with the means overplotted
boxplot(sv17_soil$Na.pow ~ sv17_soil$Reserve,
        notch=F, col="thistle",
        xlab="Reserve", ylab="Na (power-transformed)")
# make a temporary object 'meanz' containing the means
meanz <- tapply(sv17_soil$Na.pow, sv17_soil$Reserve, mean, na.rm=T)
# plot means as points (boxplot boxes are centered on whole numbers)
points(seq(1, nlevels(sv17_soil$Reserve)), meanz,
       col = 6, pch = 3, lwd = 2)
legend("bottomright", "Mean values",
       pch = 3, pt.lwd = 2, col = 6,
       bty = "n", inset = 0.03)
mtext("(c)", 3, -1.5, adj=0.03, font=2)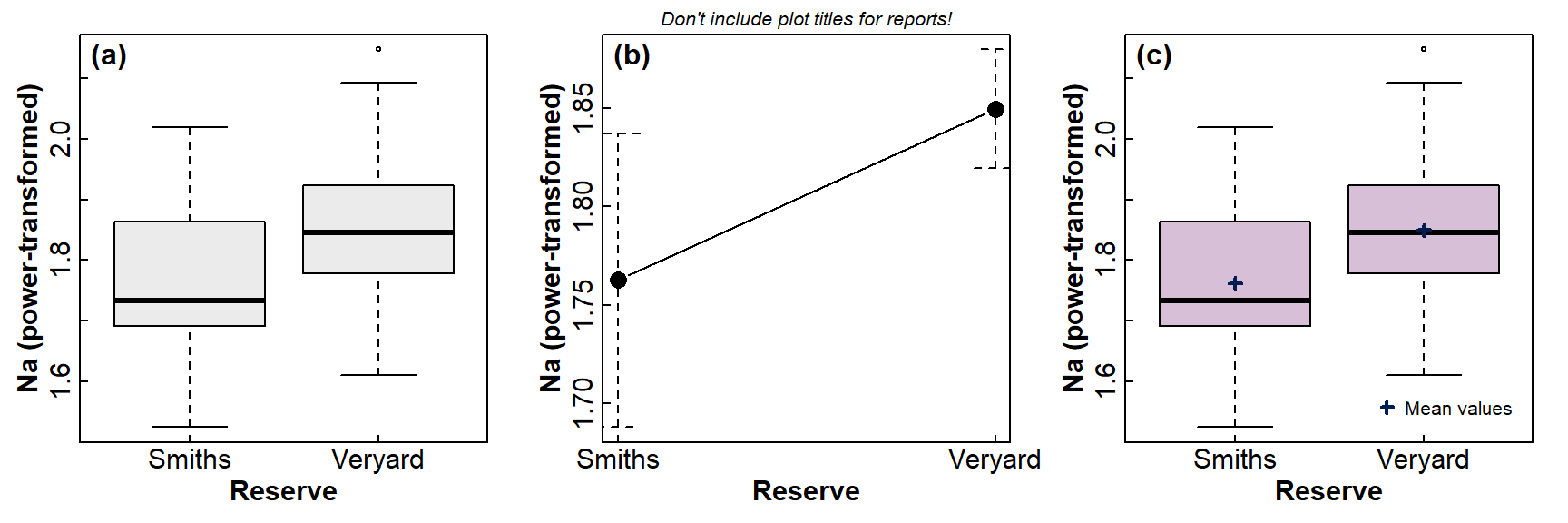

Figure 3: Graphical comparison of means between groups using: (a) a standard box plot; (b) a plot of means showing 95% CI; (c) a box plot also showing mean values in each group.

rm(meanz) # tidy up

[skip to Figure 5 for a 3-group comparison]

Homogeneity of variance using the variance ratio test or Bartlett's Test

We can actually check if the variances are equal in each group using Bartlett's Test (bartlett.test()), or for this example with exactly two groups we can use the var.test() function (do they both give the same conclusion?):

with(sv17_soil, bartlett.test(Na.pow ~ Reserve))
with(sv17_soil, var.test(Na.pow ~ Reserve))

##
##  Bartlett test of homogeneity of variances
##
## data:  Na.pow by Reserve
## Bartlett's K-squared = 1.6001, df = 1, p-value = 0.2059
##
##
##  F test to compare two variances
##
## data:  Na.pow by Reserve
## F = 1.664, num df = 15, denom df = 51, p-value = 0.1789
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.7911095 4.2363994
## sample estimates:
## ratio of variances
##           1.663991

Both the variance-ratio and Bartlett tests show that H₀ (that variances are equal) can not be rejected. We can visualise this with (for instance) a boxplot or density plot (Figure 4):

require(car)
par(mfrow=c(1,2), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.6,0.5,0),
    font.lab=2, font.main=3, cex.main=0.8, tcl=-0.2,
    cex.lab = 1, cex.axis = 1)
boxplot(sv17_soil$Na.pow ~ sv17_soil$Reserve,
        notch=FALSE, col="grey92",
        xlab="Reserve", ylab="Na (power-transformed)")
densityPlot(sv17_soil$Na.pow ~ sv17_soil$Reserve,
            xlab="Na (power transformed)", adjust=1.5, ylim=c(0,5))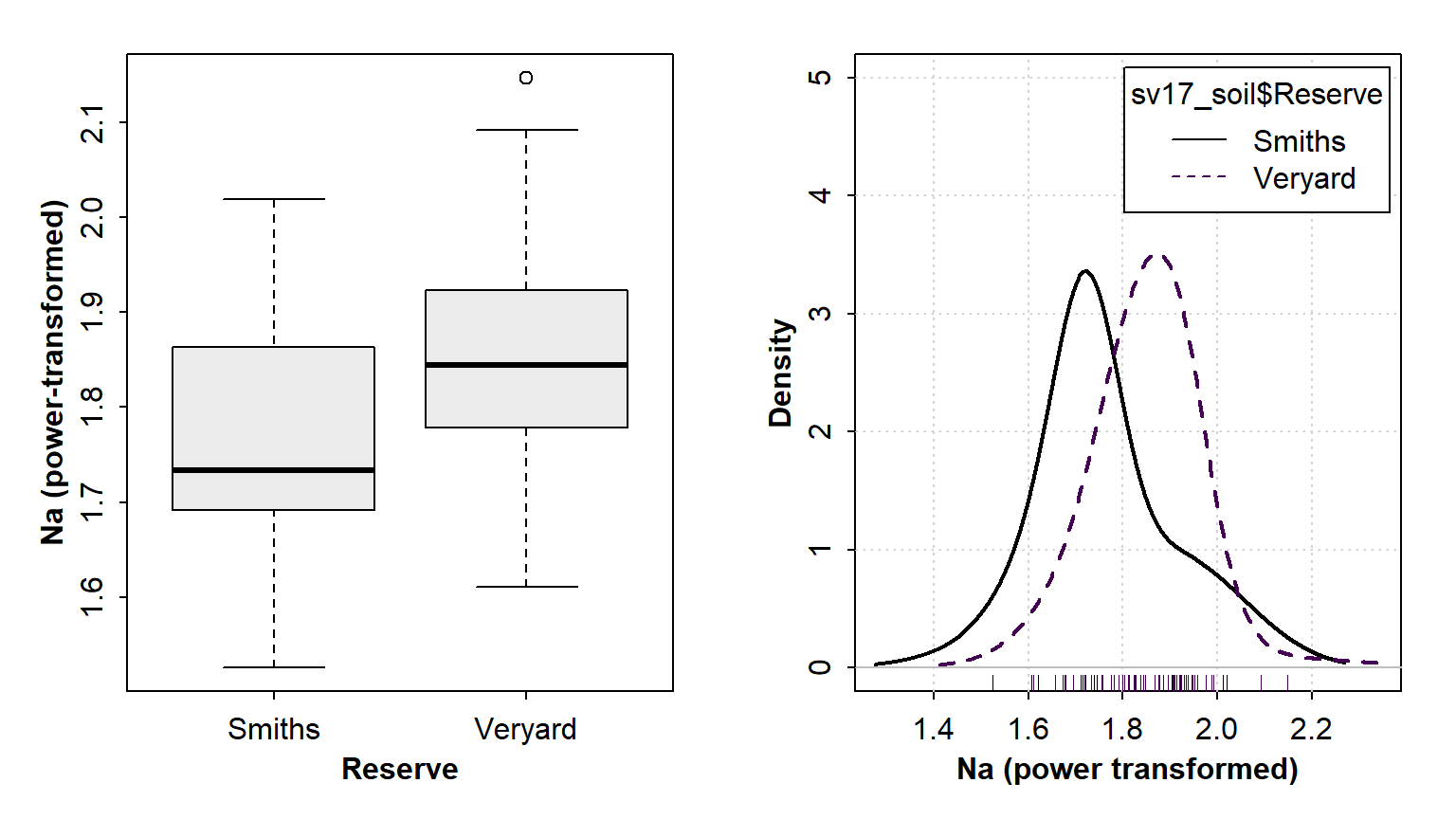

Figure 4: Graphical visulaization of variance (the 'spread' of the distribution) in each group using (left) a box plot and (right) a density plot.

par(mfrow=c(1,1)) # reset multiple graphics panes

In each case it's apparent that the variance in Na in the Veryard soil is similar to that at Smith's Lake, illustrating the conclusion from the statistical tests.

Effect size for means comparisons: Cohens d

Statistical tests which compare means only estimate if there is a difference or not. We would also usually like to know how big the difference (or 'effect') is! The Cohen's d statistic is a standardised measure of effect size available in the effsizeh R package.

require(effsize)
cohen.d(sv17_soil$Na.pow ~ sv17_soil$Reserve)

##
## Cohen's d
##
## d estimate: -0.7483083 (medium)
## 95 percent confidence interval:
##      lower      upper
## -1.3332988 -0.1633178

The calculated value of Cohen's d is 0.5 ≤ d < 0.8, which is medium. The 95% CI for the estimate of Cohen's d (i.e. between lower and upper) does not include zero, so we can probably rely on it.

More recently than Cohen, Sawilowsky (2009) proposed that for Cohen's d:

0.01 ≤	d	< 0.2	very small
0.2 ≤	d	< 0.5	small
0.5 ≤	d	< 0.8	medium
0.8 ≤	d	< 1.2	large
1.2 ≤	d	< 2.0	very large
	d	> 2.0	huge

Means comparisons for 3 or more groups

If we have a factor with 3 or more levels (a.k.a. groups, or categories), we can use analysis of variance (ANOVA) to compare means of a normally distributed variable. In this example we'll use the factor 'Type' (= sample type) from the Smith's -- Veryard data (not just soil!).
We still need to use appropriately transformed variables!

require(car)
powerTransform(sv2017$Al)
sv2017$Al.pow <- (sv2017$Al)^0.455
anova_Al <- aov(sv2017$Al.pow ~ sv2017$Type)
print(anova_Al$call)
summary(anova_Al)
cat("\nMeans for transformed variable\n");
meansAl <- tapply(sv2017$Al.pow, sv2017$Type, mean, na.rm=TRUE);
print(signif(meansAl,3)) # output means with appropriate significant digits
cat("\nMeans for original (untransformed) variable\n");
meansAl <- tapply(sv2017$Al, sv2017$Type, mean, na.rm=TRUE);
print(signif(meansAl,4)) # output means with appropriate significant digits
rm(list=c("anova_Al","meansAl")) # tidy up

## Estimated transformation parameter
## sv2017$Al
## 0.4552982
## aov(formula = sv2017$Al.pow ~ sv2017$Type)
##             Df Sum Sq Mean Sq F value Pr(>F)
## sv2017$Type  2  299.3  149.63   4.163 0.0189 *
## Residuals   85 3055.5   35.95
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 7 observations deleted due to missingness
##
## Means for transformed variable
##    Sediment        Soil Street dust
##        30.6        35.8        34.2
##
## Means for original (untransformed) variable
##    Sediment        Soil Street dust
##        2083        2667        2380

In the output above, the p-value in the ANOVA table Pr(>F) is less than 0.05 allowing us to reject the null hypothesis. As for a two-group comparison, we can visualize the differences in means in different ways (Figure 5).

Visualising differences in means - 3 or more groups

par(mfrow=c(1,3), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.7,0.3,0),
    font.lab=2, font.main=3, cex.main=1, tcl=0.3,
    cex.lab = 1.4, cex.axis = 1.4, lend = "square", ljoin = "mitre")
boxplot(sv2017$Al.pow ~ sv2017$Type, notch=T,
        cex = 1.2, col="grey92", ylim = c(15,61),
        xlab="Sample type", ylab="Al (power-transformed)")
mtext("(a)", 3, -1.5, adj=0.97, font=2) # label each sub-plot
require(RcmdrMisc)
plotMeans(sv2017$Al.pow, sv2017$Type, error.bars="conf.int",
        xlab="Sample type", ylab="Al (power-transformed)",
        main = "Don't include plot titles in reports!",
        ylim = c(15,61))
mtext("(b)", 3, -1.5, adj=0.97, font=2) # label each sub-plot
boxplot(sv2017$Al.pow ~ sv2017$Type, notch=F,
        col=c("cadetblue","moccasin","thistle"),
        cex = 1.2, ylim = c(15,61),
        xlab="Reserve", ylab="Al (power-transformed)")
mtext("(c)", 3, -1.5, adj=0.97, font=2) # label each sub-plot
meanz <- tapply(sv2017$Al.pow, sv2017$Type, mean, na.rm=T)
points(seq(1, nlevels(sv2017$Type)), meanz,
       col = "white", pch = 3, lwd = 4, cex = 1.3)
points(seq(1, nlevels(sv2017$Type)), meanz,
       col = "red3", pch = 3, lwd = 2, cex = 1.2)
legend("bottomright", "Mean values",
       pch = 3, pt.lwd = 2, col = "red3", pt.cex = 1.2,
       bty = "n", inset = 0.03)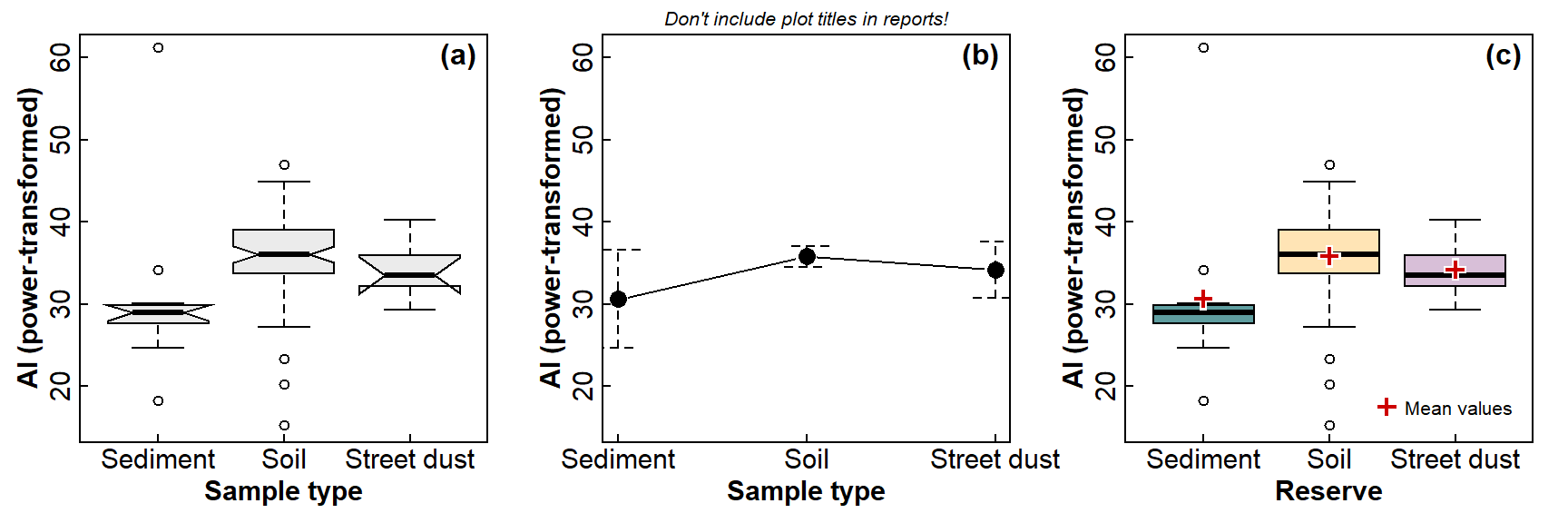

Figure 5: Graphical comparison of means between 3 or more groups, in three ways: (a) a notched box plot; (b) a plot of means with 95% CI error bars; (c) a box plot also showing mean values in each group.

rm(meanz) # tidy up

Look back at Figure 4. Why is Figure 5 better?

Check homogeneity of variances, 3 or more groups

ANOVA also requires variance for each group to be (approximately) equal. Since there are more than 2 groups, we need to use the Bartlett test.

bartlett.test(sv2017$Al.pow~sv2017$Type)

##
##  Bartlett test of homogeneity of variances
##
## data:  sv2017$Al.pow by sv2017$Type
## Bartlett's K-squared = 12.85, df = 2, p-value = 0.001621

require(car)
par(mfrow=c(1,2), mar=c(3.5,3.5,1.5,1.5), mgp=c(1.6,0.5,0),
    font.lab=2, font.main=3, cex.main=0.8, tcl=-0.2,
    cex.lab = 1, cex.axis = 1)
boxplot(sv2017$Al.pow ~ sv2017$Type,
        notch=FALSE, col="grey92",
        xlab="Reserve", ylab="Al (power-transformed")
densityPlot(sv2017$Al.pow ~ sv2017$Type, adjust=2,
            xlab="Al (power transformed)")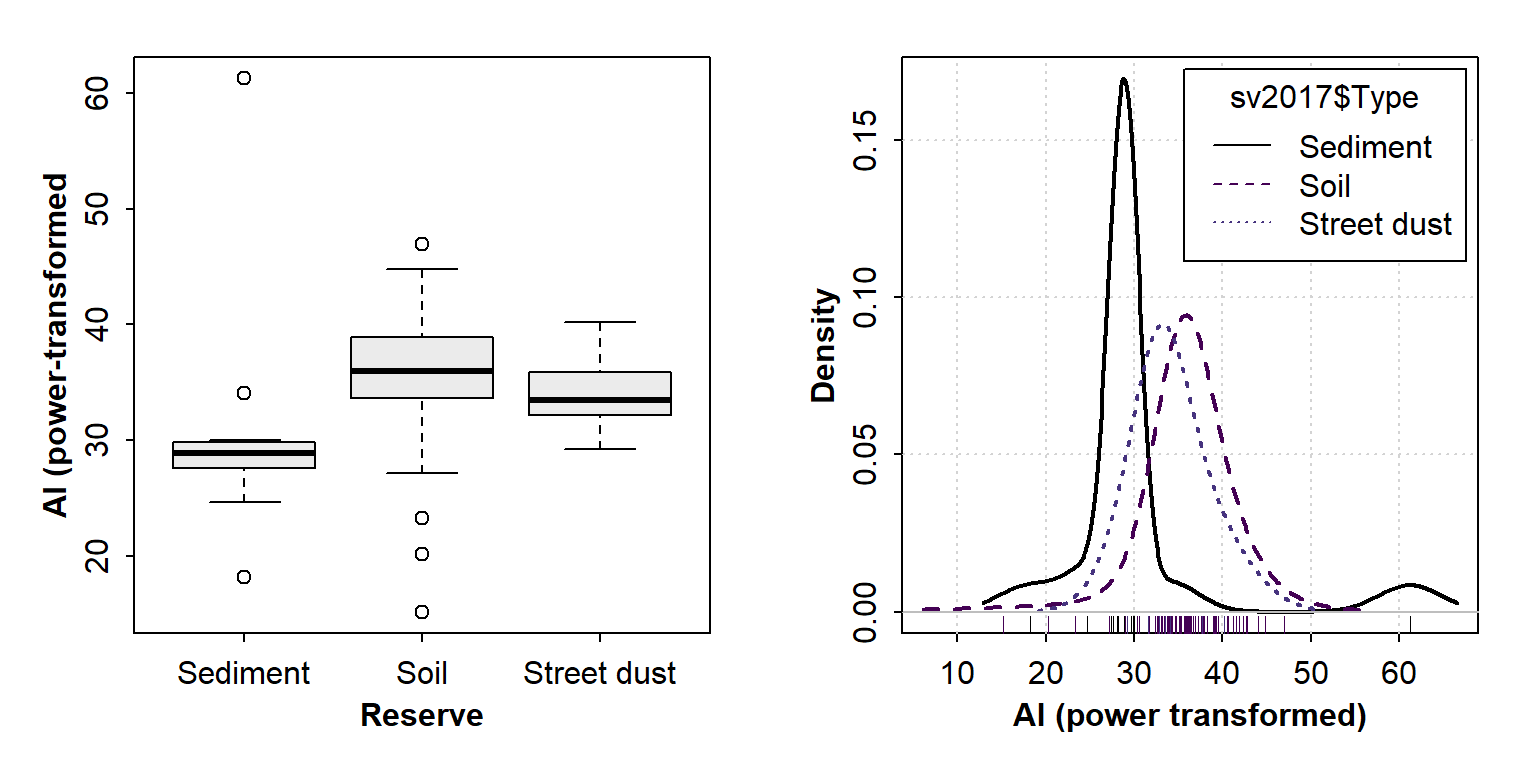

Figure 6: Graphical visualization of variance (the 'spread' of the distribution) in 3 groups using (left) a box plot and (right) a density plot.

par(mfrow=c(1,1)) # reset multiple graphics panes

In each case it's apparent that the variance in Al is Sediment > Street dust > soil (Figure 5). We can check the actual variance values using tapply():

cat("--- Variances for each factor level ---\n")
with(sv2017, tapply(Al.pow, Type, var, na.rm=TRUE))

## --- Variances for each factor level ---
##    Sediment        Soil Street dust
##    98.10216    26.80443    13.72370

"The analysis of variance is not a mathematical theorem, but rather a convenient method of arranging the arithmetic."

--- Ronald Fisher, the developer of ANOVA

Analysis of variance with unequal variances (heteroskedastic variable)

We can compare means using the Welch f-test (oneway.test()) if our variable has different variance for different factor levels.

with(sv2017, oneway.test(Al.pow ~ Type))

##
##  One-way analysis of means (not assuming equal variances)
##
## data:  Al.pow and Type
## F = 1.9945, num df = 2.000, denom df = 13.702, p-value = 0.1737

The Welch correction for unequal variances means the p-value is now too high to reject the null hypothesis, so we find no difference between means.

Effect sizes for 3 or more groups

It's not possible to calculate Effect sizes for 3 or more groups directly. We would need to create subsets of our dataset which include only two groups (e.g., with only Soil and Sediment), and then run cohen.d() from the 'effsize' R package. Or we could do some custom coding...

Pairwise comparisons

If our analysis of variance allows rejection of H₀, we still don't necessarily know which means are different. The test may return a p-value ≤ 0.05 even if only one mean is different from all the others. If the p-value ≤ 0.05, we can compute Pairwise Comparisons. The examples below show pairwise comparisons in an analysis of variance for Ba, in groups defined by the factor Type.

The most straightforward way to conduct pairwise comparisons is with the pairwise.t.test() function -- this is what we recommend. We can generate the convenient 'compact letter display' using the R packages rcompanion and multcompView. With the compact letter display, factor levels (categories) having the same letter are not significantly different (pairwise p ≥ 0.05).

Note that pairwise comparisons always adjust p-values to greater values, to account for the increased likelihood of Type 1 Error (false positives) with multiple comparisons. There are several ways of making this correction, such as Holm's method.

First, we know we can apply a post-hoc pairwise test, since the overall effect of Type on Ba is significant (p ≈ 0.002):

with(sv2017, shapiro.test(Ba.log))
with(sv2017, bartlett.test(Ba.log ~ Type))
anovaBa <- with(sv2017, aov(Ba.log ~ Type))
cat("==== Analysis of Variance ====\n");summary(anovaBa)

##
##  Shapiro-Wilk normality test
##
## data:  Ba.log
## W = 0.9885, p-value = 0.6358
##
##
##  Bartlett test of homogeneity of variances
##
## data:  Ba.log by Type
## Bartlett's K-squared = 3.4694, df = 2, p-value = 0.1765
##
## ==== Analysis of Variance ====
##             Df Sum Sq Mean Sq F value  Pr(>F)
## Type         2  0.538 0.26919    6.66 0.00206 **
## Residuals   85  3.436 0.04042
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 7 observations deleted due to missingness

How did we get Ba.log? (You need to calculate it yourself with a line of R code!). Also, what do the Shapiro-Wilk and Bartlett tests tell us about our choice of means comparison test?

Next we generate the compact letters using the fullPTable() function from the rcompanion package and multcompLetters() from the multcompView package:

library(rcompanion)
library(multcompView)
(pwBa <- with(sv2017, pairwise.t.test(Ba.log, Type)))
cat("\n==== Compact letters ====\n")
pwBa_pv <- fullPTable(pwBa$p.value)                 # from rcompanion
multcompLetters(pwBa_pv)                            # from multcompView

##
##  Pairwise comparisons using t tests with pooled SD
##
## data:  Ba.log and Type
##
##             Sediment Soil
## Soil        0.0031   -
## Street dust 0.0078   0.3634
##
## P value adjustment method: holm
##
## ==== Compact letters ====
##    Sediment        Soil Street dust
##         "a"         "b"         "b"

In the output above, the table of p-values show a significant difference (p < 0.05) between Sediment and Soil, and Sediment and Street dust (note the use of Holm's p-value adjustment, which is the default method). We get the same interpretation from the compact letters; Sediment ("a") is different from Soil and Street dust (both "b"). Since Soil and Street dust have the same letter ("b"), they are not significantly different, which matches the p-value (0.3634).

OPTIONAL: Pairwise compact letter display

This method using the cld() function is way harder to make sense of... it's probably more rigorous, but leads to the same conclusion. We need to load the multcomp package.

require(multcomp)
pwise0 <- glht(anovaBa, linfct = mcp(Type="Tukey")) # anovaBa from above
cld(pwise0)

##    Sediment        Soil Street dust
##         "a"         "b"         "b"

Groups assigned a different letter are significantly different at the specified probability level (p ≤ 0.05 by default). In this example, Ba concentration in sediment (a) is significantly different from both Soil and Street dust (both b, so not different from each other).

We can get the confidence intervals and p-values for each pairwise comparison using the TukeyHSD() function (HSD='Honestly Significant Difference'):

OPTIONAL: Pairwise Tukey multiple comparisons of means

Also more complicated to understand and, like the code above, we need to have a normally-distributed, homoskedastic, variable. Usually we don't.

TukeyHSD(anovaBa)

rm(list=c("anovaBa","pwise0"))    # tidy up

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
##
## Fit: aov(formula = Ba.log ~ Type)
##
## $Type
##                            diff         lwr       upr     p adj
## Soil-Sediment        0.20660696  0.06143156 0.3517824 0.0029746
## Street dust-Sediment 0.27953479  0.05469616 0.5043734 0.0108295
## Street dust-Soil     0.07292783 -0.11744448 0.2633002 0.6331075

The first table of output from TukeyHSD() (after $Type) shows the differences between mean values for each pairwise comparison (diff), and the lower (lwr) and upper (upr) limits of the 95% confidence interval for the difference in means. If the 95% CI includes zero (e.g. for the Street dust-Soil comparison above), there is no significant difference.

This conclusion is supported by the last column of output, showing an adjusted p-value of 0.633 (i.e. > 0.05) for the Street dust-Soil comparison. Also, as indicated by the 'compact letter display' from cld() above, any comparison including Sediment has p ≤ 0.05.

Non-Parametric Comparisons

1. Wilcoxon test

From previous sessions we know that most untransformed variables are not normally distributed. For comparison between exactly 2 groups we use the Wilcoxon test (via the wilcox.test() function). The Wilcoxon test is based on ranking of observations, so should be independent of transformation -- as in the example below:

wilcox.test(sv17_soil$Na ~ sv17_soil$Reserve)
{cat("Means for original (untransformed) variable\n")
meansNa <- tapply(sv17_soil$Na, sv17_soil$Reserve, mean,
                  na.rm=TRUE)
print(signif(meansNa, 3))
cat("\n--------------------------------------------\n")}
wilcox.test(sv17_soil$Na.pow ~ sv17_soil$Reserve)
{cat("Means for transformed variable\n")
meansNa <- tapply(sv17_soil$Na.pow, sv17_soil$Reserve, mean, na.rm=TRUE)
print(signif(meansNa, 3))}
rm(meansNa) # remove temporary object(s)

##
##  Wilcoxon rank sum test with continuity correction
##
## data:  sv17_soil$Na by sv17_soil$Reserve
## W = 246, p-value = 0.01426
## alternative hypothesis: true location shift is not equal to 0
##
## Means for original (untransformed) variable
##  Smiths Veryard
##     102     139
##
## --------------------------------------------
##
##  Wilcoxon rank sum test with continuity correction
##
## data:  sv17_soil$Na.pow by sv17_soil$Reserve
## W = 246, p-value = 0.01426
## alternative hypothesis: true location shift is not equal to 0
##
## Means for transformed variable
##  Smiths Veryard
##    1.76    1.85

Effect size

require(effsize)
cohen.d(sv17_soil$Na.pow ~ sv17_soil$Reserve)

##
## Cohen's d
##
## d estimate: -0.7483083 (medium)
## 95 percent confidence interval:
##      lower      upper
## -1.3332988 -0.1633178

2. Kruskal-Wallis test

We use the Kruskal-Wallis test (via the kruskal.test() function) for non-parametric comparisons between three or more groups defined by a factor.

This example is testing differences in Fe between sample Types in the complete Smith's -- Veryard 2017 dataset.

kruskal.test(sv2017$Fe ~ sv2017$Type)
{cat("Means for original (untransformed) variable\n")
meansFe <- tapply(sv2017$Fe, sv2017$Type, mean,
                  na.rm=TRUE)
print(signif(meansFe),4)}
rm(meansFe)

##
##  Kruskal-Wallis rank sum test
##
## data:  sv2017$Fe by sv2017$Type
## Kruskal-Wallis chi-squared = 8.222, df = 2, p-value = 0.01639
##
## Means for original (untransformed) variable
##    Sediment        Soil Street dust
##        5111        2695        3694

With a p-value of ≈ 0.016, H₀ can be rejected. We still have the problem of not knowing which means are significantly different from each other. The PMCMRplus R package allows multiple comparisons of means following statistically significant Kruskal-Wallis comparisons (there are several options; we will use the Conover's non-parametric all-pairs comparison test for Kruskal-type ranked data).

Pairwise comparisons following a Kruskal-Wallis test

require(PMCMRplus)
kwAllPairsConoverTest(Fe~Type, data=sv2017)

##
##  Pairwise comparisons using Conover's all-pairs test

## data: Fe by Type

##
## P value adjustment method: single-step

##             Sediment Soil
## Soil        0.927    -
## Street dust 0.064    0.010

The pairwise comparisons show that only Soil and Street dust have significantly different Fe concentration. Note the p-value adjustment -- not Holm's this time.

We can also get a pairwise compact letter display based on the results of non-parametric tests. As before, we need the R packages rcompanion and multcompView to do this easily.

library(rcompanion)
library(multcompView)
pwFe_Type <- with(sv2017, kwAllPairsConoverTest(Fe ~ Type)) # from PMCMRplus
pwFe_Type_pv <- fullPTable(pwFe_Type$p.value)               # from rcompanion
multcompLetters(pwFe_Type_pv)                               # from multcompView

##    Sediment        Soil Street dust
##        "ab"         "a"         "b"

The output from kwAllPairsConoverTest() shows that p ≤ 0.05 only for the Soil-Street dust comparison ("ab" matches "a" OR "b"). We can't reject H₀ for any other pairwise comparisons. [We would get slightly different results using the functions kwAllPairsDunnTest() or kwAllPairsNemenyiTest() - see below. In this example, the conclusions are the same for each type of pairwise test, but this isn't always the case.]

kwAllPairsDunnTest(Fe~Type, data=sv2017)
kwAllPairsNemenyiTest(Fe~Type, data=sv2017)

##
##  Pairwise comparisons using Dunn's all-pairs test

## data: Fe by Type

##
## P value adjustment method: holm

## alternative hypothesis: two.sided

##             Sediment Soil
## Soil        0.721    -
## Street dust 0.056    0.012

##
##  Pairwise comparisons using Tukey-Kramer-Nemenyi all-pairs test with Tukey-Dist approximation

## data: Fe by Type

##
## P value adjustment method: single-step

## alternative hypothesis: two.sided

##             Sediment Soil
## Soil        0.932    -
## Street dust 0.072    0.012

References and R Packages

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). New York:Academic Press.

Sawilowsky, S.S. (2009). New Effect Size Rules of Thumb. Journal of Modern Applied Statistical Methods 8:597-599.

Run the R code below to get citation information for the R packages used in this document.

citation("car", auto = TRUE)
citation("RcmdrMisc", auto = TRUE)
citation("effsize", auto = TRUE)
citation("multcomp", auto = TRUE)
citation("PMCMRplus", auto = TRUE)
citation("rcompanion", auto = TRUE)
citation("multcompView", auto = TRUE)

CC-BY-SA • All content by Ratey-AtUWA. My employer does not necessarily know about or endorse the content of this website.
Created with rmarkdown in RStudio using the cyborg theme from Bootswatch via the bslib package, and fontawesome v5 icons.